집단 유전학은 집단 안팎의 유전적 차이를 다루는 유전학의 하위 분야이며, 진화생물학의 일부이다. 이 생물학 분야의 연구는 적응, 종분화 및 인구 구조와 같은 현상을 조사합니다. [1]
집단 유전학은 현대 진화 합성의 출현에 중요한 요소였다. 주요 창립자는 Sewall Wright, J. B. S. Haldane 및 Ronald Fisher였으며 양적 유전학의 관련 분야의 토대를 마련했습니다. 전통적으로 고도의 수학적 학문 인 현대 인구 유전학은 이론, 실험실 및 현장 작업을 포함합니다. 집단 유전 모델은 DNA 서열 데이터로부터의 통계적 추론과 개념의 증명/반증에 둘 다 사용된다. [2]
진화 게임 이론 및 적응 역학과 같은 진화를 모델링하는 데 대한 새롭고 표현형 적 접근법과 인구 유전학을 차별화하는 것은 지배력, epistasis, 유전 적 재조합이 연결 불균형을 깨뜨리는 정도, 돌연변이 및 유전 적 표류의 무작위 현상과 같은 유전 현상에 중점을 둡니다. 이것은 집단 유전체학 데이터와 비교하는 데 적합합니다.
목차
역사[편집]
인구 유전학은 멘델 상속과 생물 통계 모델의 화해로 시작되었습니다. 자연 선택은 집단에 충분한 유전 적 변이가있는 경우에만 진화를 일으킬 것입니다. 멘델 유전학이 발견되기 전에, 한 가지 공통된 가설은 상속을 혼합하는 것이 었습니다. 그러나 혼합 상속으로 인해 유전 적 차이가 급속히 상실되어 자연 또는 성적 선택에 의한 진화가 불가능해질 것입니다. Hardy-Weinberg 원칙은 Mendelian 상속을 가진 인구에서 변동이 어떻게 유지되는지에 대한 해결책을 제공합니다. 이 원리에 따르면, 대립 유전자의 빈도 (유전자의 변이)는 선택, 돌연변이, 이동 및 유전 적 표류가없는 경우 일정하게 유지됩니다. [3]
다음 핵심 단계는 영국의 생물학자이자 통계학자인 로널드 피셔(Ronald Fisher)의 연구였다. 피셔는 1918년부터 1930년에 출간된 그의 저서 『자연선택의 유질이론』(The Genetical Theory of Natural Selection)에서 절정에 달한 일련의 논문에서 생체 인식 학자들에 의해 측정된 연속적인 변이가 많은 개별 유전자의 결합 작용에 의해 생성될 수 있고, 자연선택이 집단의 대립유전자 빈도를 변화시켜 진화를 가져올 수 있음을 보여주었다. 1924 년에 시작된 일련의 논문에서 영국의 또 다른 유전 학자 J. B. S. Haldane은 광범위한 조건 하에서 단일 유전자 유전자좌에서 대립 유전자 빈도 변화의 수학을 연구했습니다. Haldane은 또한 후추 나방 진화 및 산업 멜라니즘과 같은 자연 선택의 실제 사례에 통계 분석을 적용했으며, 선택 계수가 피셔가 가정 한 것보다 클 수 있음을 보여 주어 오염 증가에 따른 위장 전략으로보다 빠른 적응 진화를 이끌어 냈습니다. [4][5]
동물 사육 실험에 대한 배경을 가진 미국의 생물 학자 세월 라이트 (Sewall Wright)는 상호 작용하는 유전자의 조합과 유전 적 표류를 보이는 작고 상대적으로 고립 된 집단에 대한 근친 교배의 영향에 중점을 두었습니다. 1932년 라이트는 적응형 풍경의 개념을 도입하고 유전적 표류와 근친 교배가 작고 고립된 하위 집단을 적응 피크로부터 멀어지게 하여 자연선택이 다른 적응 피크로 이끌 수 있다고 주장했다. [인용 필요]
Fisher, Haldane 및 Wright의 연구는 인구 유전학의 분야를 설립했습니다. 이 통합 된 자연 선택은 멘델 유전학과 통합되었으며, 이는 진화가 어떻게 작동하는지에 대한 통일 된 이론을 개발하는 데 중요한 첫 번째 단계였습니다. [4][5] 존 메이너드 스미스는 할단의 제자였고, W. D. 해밀턴은 피셔의 저술에 영향을 받았다. 미국의 조지 R. 프라이스는 해밀턴과 메이너드 스미스와 함께 일했다. 미국의 리처드 레원틴과 일본의 모투 키무라는 라이트와 할단의 영향을 받았다. [인용 필요]
현대 합성[편집]
인구 유전학의 수학은 원래 현대 합성의 시작으로 개발되었습니다. Beatty[6]와 같은 저자들은 집단 유전학이 현대 합성의 핵심을 정의한다고 주장했다. 20세기의 처음 수십 년 동안, 대부분의 현장 자연주의자들은 라마르키즘과 정통성이 살아있는 세계에서 관찰된 복잡성에 대한 최상의 설명을 제공한다고 계속 믿었다. [7] 현대 종합 동안, 이러한 관념들은 제거되었고, 집단 유전학의 수학적 틀에서 표현될 수 있는 진화적 원인들만이 유지되었다. [8] 진화적 요인들이 진화에 영향을 미칠 수 있는 것에 대해서는 합의가 이루어졌지만, 다양한 요소들의 상대적 중요성에 대해서는 도달하지 못했다. [8]
T. H. Morgan의 실험실에서 박사후 연구원 인 Theodosius Dobzhansky는 Sergei Chetverikov와 같은 러시아 유전 학자들의 유전 적 다양성에 관한 연구에 영향을 받았다. 그는 인구 유전학자들이 개발한 미진화의 기초와 현장 생물학자들이 관찰한 대진화의 패턴 사이의 분열을 해소하는 데 도움을 주었고, 1937년 그의 저서 《유전학과 종의 기원》을 통해 말이다. Dobzhansky는 야생 개체군의 유전 적 다양성을 조사하고 인구 유전 학자들의 가정과는 달리이 집단은 많은 양의 유전 적 다양성을 가지고 있으며 하위 집단간에 현저한 차이가 있음을 보여주었습니다. 이 책은 또한 인구 유전 학자들의 고도로 수학적 인 연구를 취하여보다 접근하기 쉬운 형태로 만들었습니다. 더 많은 생물학자들이 도브잔스키를 통해 집단 유전학의 영향을 받았는데, 이는 원작에서 매우 수학적인 작품을 읽을 수 있었던 것보다 더 많았다. [9]
영국에서는 생태 유전학의 선구자인 E. B. 포드[10]가 1930년대와 1940년대에 걸쳐 인간 혈액형과 같은 유전적 다형성을 통해 유전적 다양성을 유지하는 능력을 포함한 생태적 요인으로 인한 선택의 힘을 경험적으로 입증하기 위해 계속되었다. . 포드의 연구는 피셔와 협력하여 현대 합성 과정에서 지배적 인 힘으로서의 자연 선택을 향한 강조의 전환에 기여했습니다. [4][5][11][12]
중립 이론과 기원 고정 역학[편집]
집단 유전학에 대한 원래의 현대 합성 견해는 돌연변이가 충분한 원료를 제공한다고 가정하고 집단 내 대립 유전자의 빈도 변화에만 초점을 맞 춥니 다. [13] 대립유전자 빈도에 영향을 미치는 주요 과정은 자연 선택, 유전자 표류, 유전자 흐름 및 재발 돌연변이입니다. 피셔와 라이트는 선택과 표류의 상대적 역할에 대해 근본적인 의견 차이가 있었다. [14] 모든 유전적 차이에 대한 분자 데이터의 가용성은 분자 진화의 중립 이론으로 이어졌다. 이 견해에서, 많은 돌연변이는 해롭고 결코 관찰되지 않으며, 나머지 대부분은 중립적이며, 즉 선택 중이 아닙니다. 각 중립 돌연변이의 운명이 우연에 맡겨지면(유전적 표류), 진화적 변화의 방향은 돌연변이가 발생하는 것에 의해 주도되며, 따라서 (기존의) 대립유전자의 빈도 변화만으로 변화의 모델에 의해 포착될 수 없다. [13][15]
집단 유전학의 기원 고정 관점은 엄격하게 중립적 인 돌연변이를 넘어이 접근법을 일반화하고, 특정 변화가 일어나는 속도를 돌연변이 속도와 고정 확률의 산물로 본다. [13]
네 가지 프로세스[편집]
선택[편집]
성적 선택을 포함하는 자연 선택은 일부 특성으로 인해 유기체가 생존하고 번식 할 가능성이 높다는 사실입니다. 집단 유전학은 적합성을 특정 환경에서의 생존 및 번식의 성향 또는 확률로 정의함으로써 자연 선택을 설명합니다. 적합성은 일반적으로 기호 w=1-s에 의해 주어지며, 여기서 s는 선택 계수입니다. 자연 선택은 표현형에 작용하므로 집단 유전 모델은 표현형을 예측하기 위해 비교적 간단한 관계를 가정하고 따라서 하나 또는 소수의 유전자좌에서 대립 유전자로부터의 적합성을 예측합니다. 이런 식으로, 자연 선택은 다른 표현형을 가진 개인의 적합성의 차이를 연속적인 세대에 걸쳐 집단의 대립 유전자 빈도의 변화로 변환합니다. [인용 필요]
집단 유전학이 출현하기 전에 많은 생물 학자들은 적합성의 작은 차이가 진화에 큰 차이를 만들기에 충분하다는 것을 의심했다. [9] 인구 유전학자들은 선택을 유전적 표류와 비교함으로써 이러한 우려를 부분적으로 해결했다. 선택은 s가 1보다 클 때 효과적인 인구 크기로 나눈 유전 적 표류를 극복 할 수 있습니다. 이 기준이 충족될 때, 새로운 유리한 돌연변이가 고정될 확률은 대략 2s와 같다. [16][17] 그러한 대립 유전자가 고정될 때까지의 시간은 유전적 표류에 거의 의존하지 않으며, log(sN)/s에 대략 비례한다.[18]
지배[편집]
우세는 유전자좌에서 한 대립 유전자의 표현형 및 / 또는 적합성 효과가 그 유전자좌에 대한 두 번째 사본에 존재하는 대립 유전자에 달려 있음을 의미합니다. 한 유전자좌에서 세 가지 유전자형을 고려하고 다음과 같은 적합성 값을 가지고 있다.[19]
| 유전자 형: | A1 A1 | A1A2 | A2 A2 |
| 상대 체력: | 1 | 1시간 | 3-1 |
s는 선택 계수이고 h는 우위 계수입니다. h 값은 다음 정보를 산출합니다.
| h = 0 | 지배 1개, 열성A 2개 |
| h = 1 | 2 지배자, A1 열성 |
| 0<h<1 | 불완전한 지배력 |
| h<0 | 과잉 지배 |
| h>1 | 지배력 저조 |
에피스타시스[편집]
epistasis는 한 유전자좌에서 대립 유전자의 표현형 및 / 또는 피트니스 효과가 다른 유전자좌에 존재하는 대립 유전자에 달려 있음을 의미합니다. 선택은 단일 유전자좌에서 작용하는 것이 아니라 완전한 유전자형으로부터의 발달을 통해 발생하는 표현형에 작용한다. [20] 그러나 성 종의 많은 집단 유전학 모델은 "단일 유전자좌"모델이며, 개인의 적합성은 각 유전자좌로부터의 기여의 산물로 계산됩니다.
사실, 피트니스 풍경에 대한 유전자형은 더 복잡합니다. 집단 유전학은 이러한 복잡성을 자세히 모델링하거나 더 간단한 평균 규칙으로 포착해야합니다. 경험적으로, 유익한 돌연변이는 이미 높은 체력을 가진 유전 적 배경에 추가 될 때 더 작은 체력 이점을 갖는 경향이 있습니다 : 이것은 수익률 epistasis를 감소시키는 것으로 알려져 있습니다. [21] 해로운 돌연변이가 높은 피트니스 배경에 더 작은 체력 효과를 가질 때, 이것은 "상승 작용 epistasis"로 알려져 있습니다. 그러나, 해로운 돌연변이의 효과는 평균적으로 증식에 매우 근접한 경향이 있거나, 심지어 "길항성 epistasis"로 알려진 반대 패턴을 보일 수도 있다. [22]
상승적 epistasis는 돌연변이 부하의 제거[23] 및 성적 재생산의 진화에 대한 일부 이론의 핵심이다.
돌연변이[편집]

돌연변이는 새로운 대립 유전자의 형태로 유전 적 변이의 궁극적 인 원천입니다. 또한, 돌연변이는 돌연변이 편향, 즉 다른 돌연변이가 발생할 확률이 다를 때 진화의 방향에 영향을 줄 수 있습니다. 예를 들어, 선택과 반대 방향에있는 경향이있는 반복적 인 돌연변이는 돌연변이 - 선택 균형으로 이어질 수 있습니다. 분자 수준에서 G에서 A로의 돌연변이가 A에서 G로의 돌연변이보다 더 자주 발생하면 A를 가진 유전자형이 진화하는 경향이 있습니다. [24] 상이한 탁사에서의 상이한 삽입 대 결실 돌연변이 편향은 상이한 게놈 크기의 진화로 이어질 수 있다. [25][26] 발달 또는 돌연변이 편향은 형태학적 진화에서도 관찰되었다. [27][28] 예를 들어, 표현형-우선적 진화 이론에 따르면, 돌연변이는 결국 이전에 환경에 의해 유도되었던 형질의 유전적 동화를 야기할 수 있다. [29][30]
돌연변이 편향 효과는 다른 과정에 겹쳐진다. 선택이 두 개의 돌연변이 중 하나를 선호하지만 둘 다 갖는 것에 대한 추가적인 이점이 없다면, 가장 자주 발생하는 돌연변이는 모집단에서 고정 될 가능성이 가장 높은 돌연변이입니다. [31][32]
돌연변이는 효과가 없거나, 유전자의 산물을 변경하거나, 유전자가 기능하지 못하게 할 수 있습니다. 파리 초파리 멜라노가스터에 대한 연구에 따르면 돌연변이가 유전자에 의해 생성 된 단백질을 변화시키면 아마도 해로울 수 있으며, 이러한 돌연변이의 약 70 %는 해로운 영향을 미치고 나머지는 중성이거나 약하게 유익합니다. [33] 대부분의 기능 상실 돌연변이는 반대쪽에 대해 선택된다. 그러나 선택이 약할 때, 기능 상실에 대한 돌연변이 편향은 진화에 영향을 미칠 수 있다. [34] 예를 들어, 안료는 동물이 동굴의 어둠 속에서 살고, 잃어버리는 경향이 있을 때 더 이상 유용하지 않다. [35] 이러한 종류의 기능 상실은 돌연변이 편향 때문에 발생할 수 있으며, 함수에 비용이 들기 때문에 발생할 수 있으며, 일단 기능의 이점이 사라지면 자연 선택은 손실로 이어진다. 실험실 진화 동안 박테리아에서 다공 능력의 손실은 다공 능력을 유지하는 비용에 대한 자연 선택보다는 돌연변이 편향에 의해 야기 된 것으로 보인다. [36] 기능 상실에 대한 선택이 없을 때, 손실이 진화하는 속도는 효과적인 집단 크기보다 돌연변이 속도에 더 의존한다.[37] 이는 그것이 유전적 표류보다는 돌연변이 편향에 의해 더 많이 좌우된다는 것을 나타낸다.
돌연변이는 DNA의 큰 부분이 복제되는 것을 포함 할 수 있으며, 일반적으로 유전 적 재조합을 통해 복제됩니다. [38] 이것은 집단 내에서 카피 번호 변동으로 이어진다. 복제는 새로운 유전자를 진화시키는 원료의 주요 원천입니다. [39] 다른 유형의 돌연변이는 때때로 이전에 코딩되지 않은 DNA로부터 새로운 유전자를 생성한다. [40][41]
유전적 표류[편집]
유전 적 드리프트는 무작위 샘플링으로 인한 대립 유전자 주파수의 변화입니다. [42] 즉, 자손의 대립 유전자는 부모에있는 사람들의 무작위 표본입니다. [43] 유전적 표류는 유전자 변이체를 완전히 사라지게 할 수 있고, 따라서 유전적 변이를 감소시킬 수 있다. 생식 성공에 따라 유전자 변이를 더 흔하게 만들거나 덜 흔하게 만드는 자연 선택과는 달리,[44] 유전 적 표류로 인한 변화는 환경 적 또는 적응 압력에 의해 주도되지 않으며, 대립 유전자를 덜 흔하게 만들 가능성이 동등합니다.
유전 적 표류의 효과는 대립 유전자가 많은 사본에 존재할 때보 다 소수의 사본에 존재하는 대립 유전자에 대해 더 큽니다. 유전 적 표류의 집단 유전학은 분지화 과정 또는 대립 유전자 빈도의 변화를 설명하는 확산 방정식을 사용하여 설명됩니다. [45] 이러한 접근법은 일반적으로 인구 유전학의 라이트 피셔 (Wright-Fisher)와 모란 (Moran) 모델에 적용됩니다. 유전 적 표류가 대립 유전자에 작용하는 유일한 진화 힘이라고 가정하면, 많은 복제 된 집단에서 t 세대 이후, p 및 q의 대립 유전자 빈도로 시작하여, 그 집단에 걸친 대립 유전자 빈도의 차이는 다음과 같습니다.
{\displaystyle V_{t}\approx pq\left(1-\exp \left\{-{\frac {t}{2N_{e}}}\right\}\right).}[46]로널드 피셔 (Ronald Fisher)는 유전 적 표류가 진화에서 가장 사소한 역할을한다는 견해를 가지고 있었으며, 이것은 수십 년 동안 지배적 인 견해로 남아있었습니다. 어떤 집단 유전학의 관점도 유전 적 표류를 그 자체로 중심 역할을하지 못했지만 일부는 다른 비 선택적 힘과 함께 유전 적 표류를 중요하게 만들었습니다. Sewall Wright의 변화 균형 이론은 인구 구조와 유전 적 표류의 결합이 중요하다고 주장했다. 모투 키무라(Motoo Kimura)의 분자 진화에 대한 중립적 이론은 집단 안팎의 대부분의 유전적 차이가 중성 돌연변이와 유전적 표류의 결합에 의해 야기된다고 주장한다. [47]
진화에서 표본 추출 오류에 의한 유전 적 표류의 역할은 John H Gillespie[48]와 Will Provine,[49] 에 의해 비판 받아 왔으며,[49] 연결된 사이트에서의 선택은 샘플링 오류를 통해 전통적으로 유전 적 표류에 기인 한 작업을 수행하는 것이 더 중요한 확률적 힘이라고 주장한다. 유전자 초안의 수학적 특성은 유전 적 표류의 수학적 특성과 다릅니다. [50] 대립유전자 주파수의 무작위 변화의 방향은 세대에 걸쳐 자동상관된다. [42]
유전자 흐름[편집]
이동에 대한 물리적 장벽과 함께 개인이 움직이거나 퍼지는 제한된 경향 (vagility) 및 출생 장소 (철학)로 남아 있거나 돌아 오는 경향 때문에, 자연 개체군은 이론적 인 무작위 모델 (panmixy)에서 가정 될 수있는 것처럼 거의 모든 교배하지 않습니다. [51] 일반적으로 개인이 일반 인구에서 무작위로 선택된 사람들보다 서로 더 밀접하게 관련되어있는 지리적 범위가 있습니다. 이것은 집단이 유전적으로 구조화되는 정도로서 설명된다. [52]
유전 적 구조화는 역사적인 기후 변화, 종 범위 확장 또는 서식지의 현재 가용성으로 인한 이동으로 인해 발생할 수 있습니다. 유전자 흐름은 산맥, 바다, 사막 또는 심지어 식물 유전자의 흐름을 방해 한 중국의 만리장성과 같은 인공 구조물에 의해 방해받습니다. [53]
유전자 흐름은 개체군이나 종 간의 유전자 교환으로 구조를 무너뜨립니다. 종 내의 유전자 흐름의 예는 유기체의 이동 및 번식 후, 또는 꽃가루의 교환을 포함한다. 종 간의 유전자 전달은 하이브리드 유기체의 형성 및 수평적 유전자 전달을 포함한다. 집단 유전 모델은 어떤 집단이 서로에게서 유의미한 유전 적 고립을 보이는지 확인하고 그들의 역사를 재구성하는 데 사용될 수 있습니다. [54]
인구를 고립시키는 것은 근친 교배 우울증으로 이어진다. 개체군으로의 이동은 새로운 유전 적 변종을 도입 할 수 있으며,[55] 잠재적으로 진화 구조에 기여합니다. 개인 또는 게이머의 상당 부분이 이주하는 경우, 대립 유전자 주파수를 변경할 수도 있습니다 (예 : 마이그레이션 부하가 발생합니다). [56]
유전자 흐름의 존재하에, 아웃크로스 종의 두 개의 발산 집단 사이의 혼성화에 대한 다른 장벽이 개체군이 새로운 종이되기 위해서는 요구된다.
수평 유전자 전달[편집]
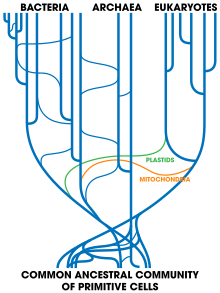
수평 유전자 전달은 한 유기체에서 그 자손이 아닌 다른 유기체로 유전 물질을 옮기는 것입니다. 이것은 원핵 생물들 사이에서 가장 흔합니다. [57] 의학에서, 이것은 한 박테리아가 저항성 유전자를 획득 할 때 다른 종으로 신속하게 옮길 수 있기 때문에 항생제 내성의 확산에 기여합니다. [58] 효모 Saccharomyces cerevisiae 및 adzuki 콩 딱정벌레 Callosobruchus chinensis와 같은 진핵 생물에 박테리아에서 유전자의 수평 전달이 또한 발생했을 수 있습니다. [59][60] 더 큰 규모의 전달의 예는 박테리아, 진균 및 식물로부터 다양한 유전자를 받은 것으로 보이는 진핵 bdelloid 회전체이다. [61] 바이러스는 또한 유기체 사이에서 DNA를 운반 할 수있어 생물학적 영역을 가로 질러 유전자를 옮길 수 있습니다. [62] 대규모 유전자 전달은 또한 엽록체와 미토콘드리아의 획득 동안, 진핵 세포와 원핵생물의 조상 사이에서 발생했다. [63]
연계[편집]
모든 유전자가 연결 평형에 있다면, 한 유전자좌에서의 대립 유전자의 효과는 다른 유전자좌의 유전자 풀에 걸쳐 평균화 될 수 있습니다. 실제로, 하나의 대립 유전자는 다른 유전자좌의 유전자와의 연결 불균형, 특히 동일한 염색체 근처에 위치한 유전자와 자주 발견됩니다. 재조합은 유전 히치 하이킹을 피하기 위해이 연결 불균형을 너무 천천히 깨뜨립니다.이 곳에서 한 유전자좌의 대립 유전자는 가까운 유전자좌에서 선택중인 대립 유전자와 연결되어 있기 때문에 높은 빈도로 상승합니다. 연계는 또한 성적 인구에서도 적응 속도를 늦춘다. [64][65][66] 적응 진화의 속도를 늦추는 데 있어서 연결 불균형의 효과는 힐-로버트슨 효과(유익한 돌연변이를 함께 가져오는 지연)와 배경 선택(해로운 히치하이커로부터 유익한 돌연변이를 분리하는 지연)의 조합으로부터 발생한다.
연결은 한 번에 하나의 유전자 유전자좌를 치료하는 집단 유전 모델에 대한 문제입니다. 그러나 선택적 스윕을 통해 자연 선택의 작용을 감지하는 방법으로 악용 될 수 있습니다.
무성애자 집단의 극단적 인 경우, 연계가 완료되고 단순한 피트니스 환경을 따라 유전자형 빈도의 이동 파동이라는 측면에서 인구 유전 방정식이 도출되고 해결 될 수 있습니다. [67] 박테리아와 같은 대부분의 미생물은 무성애자이다. 그들의 적응의 인구 유전학은 두 가지 대조적 인 정권을 가지고 있습니다. 유익한 돌연변이율과 인구 크기의 산물이 작을 때, 무성애자 집단은 기원 고정 역학의 "계승 체제"를 따르며, 적응률은이 제품에 크게 의존합니다. 제품이 훨씬 더 클 때, 무성애자 집단은 적응 속도가 제품에 덜 의존하는 "동시 돌연변이"체제를 따르며, 클론 간섭과 마지막 돌연변이가 고정되기 전에 새로운 유익한 돌연변이가 나타나는 것을 특징으로합니다.
응용 프로그램[편집]
유전자 변이의 수준 설명[편집]
중립 이론은 집단의 뉴클레오티드 다양성 수준이 집단 크기 및 중성 돌연변이율의 산물에 비례 할 것이라고 예측합니다. 유전 적 다양성의 수준이 인구 크기보다 훨씬 적게 다양하다는 사실은 "변이의 역설"로 알려져 있습니다. [68] 높은 수준의 유전 적 다양성이 중립 이론에 찬성하는 원래의 주장 중 하나였지만, 변이의 역설은 중립 이론에 대한 가장 강력한 주장 중 하나였습니다.
유전 적 다양성의 수준은 유전 적 히치 하이킹과 배경 선택으로 인해 지역 재결합 속도의 함수로서 종 내에서 크게 다르다는 것이 분명합니다. 변동의 역설에 대한 대부분의 현재 솔루션은 링크 된 사이트에서 일정 수준의 선택을 호출합니다. [69] 예를 들어, 한 분석에 따르면 더 큰 집단은 더 중립적 인 유전 적 다양성을 제거하는 더 많은 선택적 스윕을 가지고 있습니다. [70] 돌연변이율과 집단 크기 사이의 부정적인 상관관계가 또한 기여할 수 있다. [71]
생명의 역사는 인구 역사보다 유전 적 다양성에 더 많은 영향을 미치며, 예를 들어 r- 전략가들은 더 많은 유전 적 다양성을 가지고 있습니다. [69]
선택 검색[편집]
집단 유전학 모델은 어떤 유전자가 선택을 겪고 있는지 추론하는 데 사용됩니다. 한 가지 일반적인 접근법은 염색체를 따라 높은 연결 불균형과 낮은 유전 적 차이의 영역을 찾아 최근의 선택적 스윕을 탐지하는 것입니다.
두 번째 일반적인 접근법은 맥도날드 - Kreitman 테스트입니다.이 테스트는 종 (다형성) 내의 변동량을 두 유형의 부위에서 종 (치환) 간의 차이와 비교합니다. 하나는 중립적 인 것으로 가정되었습니다. 일반적으로 동의어 사이트는 중립으로 간주됩니다. [72] 양성 선택을 받는 유전자는 다형성 부위에 비해 과량의 발산 부위를 갖는다. 이 검사는 또한 양성 선택에 의해 고정되는 치환의 비율에 대한 게놈 전체 추정치를 얻기 위해 사용될 수 있다.α[73][74] 분자 진화의 중립 이론에 따르면, 이 숫자는 거의 0에 가까워야 한다. 따라서 높은 숫자는 중립 이론의 게놈 전체 위조로 해석되었습니다. [75]
인구통계학적 추론[편집]
성적으로 번식하는 이배체 종의 인구 구조에 대한 가장 간단한 테스트는 유전자형 빈도가 대립 유전자 빈도의 함수로서 Hardy-Weinberg 비율을 따르는지 여부를 확인하는 것입니다. 예를 들어, 두 개의 대립유전자가 있는 단일 유전자좌의 가장 간단한 경우, 주파수 p 및 q에서 A와 a로 표시되고, 랜덤 짝짓기는 AA 동형접합체에 대해 freq(AA) = p2, aa 동형접합체에 대한 freq(aa) = q2, 이형접합체에 대한 freq(Aa) =2pq를 예측한다. . 인구 구조가없는 경우, Hardy-Weinberg 비율은 1-2 세대의 무작위 짝짓기 내에 도달합니다. 보다 전형적으로, 인구 구조를 나타내는 동형접합체의 과잉이 있다. 이러한 과잉의 정도는 근친 교배 계수 F로서 정량화될 수 있다.
개인은 K 하위집단으로 클러스터링될 수 있다. [76][77] 집단 구조의 정도는 집단 구조에 의해 설명될 수 있는 유전적 분산의 비율의 척도인 FST를 사용하여 계산될 수 있다. 유전 집단 구조는 지리적 구조와 관련될 수 있고, 유전적 혼화제가 검출될 수 있다.
합체 이론은 표본의 유전 적 다양성을 그것이 취해진 인구의 인구 통계 학적 역사와 관련시킵니다. 그것은 일반적으로 중립성을 가정하므로 게놈의보다 중립적으로 진화하는 부분의 서열이 그러한 분석을 위해 선택됩니다. 그것은 종 (계통 유전학)뿐만 아니라 인구 구조, 인구 통계 학적 역사 (예 : 인구 병목 현상, 인구 증가), 생물학적 분산, 근원 싱크 역학 [78] 및 종 내 내성 사이의 관계를 추론하는 데 사용할 수 있습니다.
인구 통계 학적 추론에 대한 또 다른 접근법은 대립 유전자 주파수 스펙트럼에 의존합니다. [79]
유전 시스템의 진화[편집]
유전 시스템 자체를 제어하는 유전자좌가 있다고 가정함으로써, 집단 유전 모델은 지배력과 다른 형태의 견고성의 진화, 성적 재생산 및 재결합 속도의 진화, 돌연변이 속도의 진화, 진화 커패시터의 진화, 값 비싼 신호 특성의 진화, 노화의 진화를 설명하기 위해 만들어졌습니다. 그리고 협력의 진화. 예를 들어, 대부분의 돌연변이는 해롭기 때문에 종에 대한 최적의 돌연변이율은 높은 해로운 돌연변이 속도로부터의 손상과 DNA 복구 효소와 같은 돌연변이 속도를 감소시키기 위한 시스템 유지의 대사 비용 사이의 트레이드오프가 될 수 있다. [80]
이러한 모델의 한 가지 중요한 측면은 선택이 해로운 돌연변이를 제거 할만큼 충분히 강하기 때문에 선택 계수 s가 유효 모집단 크기의 역보다 큰 경우 분해에 대한 돌연변이 편향을 압도한다는 것입니다. 이것은 드리프트 장벽으로 알려져 있으며 분자 진화의 거의 중립적 인 이론과 관련이 있습니다. 드리프트 장벽 이론은 효과적인 인구 크기가 큰 종은 매우 간소화되고 효율적인 유전 시스템을 가질 것이며, 인구 크기가 작은 종은 인트론과 전이 가능한 요소를 포함하는 팽창하고 복잡한 게놈을 가질 것이라고 예측합니다. [81] 그러나 다소 역설적이게도, 큰 개체군 크기를 가진 종은 특정 유형의 오류의 결과에 너무 관대하여 작은 개체군보다 전사 및 번역과 같은 오류율이 더 높습니다. [82]
또한 보십시오[편집]
참고문헌[편집]
- ^ "인구 유전학 - 최신 연구 및 뉴스". www.nature.com. 2018년 1월 29일에 확인함.
- ^ 세르베디오, 마리아 알; 브란바인, 야니프; Dhole, Sumit; 피츠패트릭, 코트니 L.; 골드버그, 엠마 E.; 스턴, 케이틀린 A.; 반 클레브, 제레미; 예, D. 저스틴 (2014년 12월 9일). "단순한 이론이 아니라 진화 생물학에서 수학적 모델의 유용성". PLOS 생물학. 12 (12): e1002017. doi:10.1371/journal.pbio.1002017. PMC 4260780. PMID 25489940.
- ^ Ewens, W.J. (2004). 수학 인구 유전학 (제 2 판). 뉴욕 : 스프링어. ISBN 978-0-387-20191-7.
- ^ Jump up to:a ᄂ c 볼러, 피터 J. (2003). 진화 : 아이디어의 역사 (제 3 판). 버클리: 캘리포니아 대학 출판부 pp. 325-339. ISBN 978-0-520-23693-6.
- ^ Jump up to:a ᄂ c 라슨, 에드워드 제이 (2004). 진화 : 과학 이론의 놀라운 역사 (현대 도서관 ed.). 뉴욕 : 현대 도서관. 221~243쪽. ISBN 978-0-679-64288-6.
- ^ 비티, 존 (1986). "합성과 합성 이론". 과학 분야 통합. 과학과 철학. 권. 2. 스프링어 네덜란드. 125~135쪽. 도이 : 10.1007 / 978-94-010-9435-1_7. ISBN 9789024733422.
- ^ 메이어, 에른스트; Provine, William B., eds. (1998). 진화 종합 : 생물학의 통일에 대한 관점 ([New ed]. ed.). 케임브리지, 매사추세츠 : 하버드 대학 출판부. pp. 295-298. ISBN 9780674272262.
- ^ Jump up to:a b 프로바인, W. B. (1988). "진화의 진보와 삶의 의미". 진화적 진보. 시카고 대학 출판부. pp. 49-79.
- ^ Jump up to:a b 프로빈, 윌리엄 B. (1978). "1930 년대와 1940 년대의 진화 적 합성에서 수학적 인구 유전 학자의 역할". 생물학의 역사에 대한 연구. 2: 167–192. PMID 11610409.
- ^ 포드, E. B. (1975) [1964]. 생태 유전학 (제 4 판). 런던 : 채프먼과 홀. 1쪽.
- ^ 메이어, 에른스트 (1988). 생물학의 새로운 철학을 향하여: 진화론자의 관찰. 케임브리지, 매사추세츠 : 하버드 대학 출판부의 Belknap Press. 402쪽. ISBN 978-0-674-89665-9.
- ^ 메이어, 에른스트; Provine, William B., eds. (1998). 진화 종합 : 생물학의 통일에 대한 관점 ([New ed]. ed.). 매사추세츠 주 케임브리지: 하버드 대학 출판부 pp. 338-341. ISBN 9780674272262.
- ^ Jump up to:a ᄂ c 맥캔들리쉬, 데이비드 엠; Stoltzfus, Arlin (2014년 9월). "고정 확률을 이용한 진화 모델링 : 역사와 함의". 생물학의 분기 별 검토. 89 (3): 225–252. 도이 : 10.1086 / 677571. PMID 25195318. S2CID 19619966.
- ^ 크로우, 제임스 F. (2010). "Wright와 Fisher on Inhusband and Random Drift". 《Wright and Fisher on Inhusband and Random Drift》. 유전학. 184 (3): 609–611. doi : 10.1534 / genetics.109.110023. ISSN 0016-6731. PMC 2845331. PMID 20332416.
- ^ 카실라스, 소니아; 바바딜라, 안토니오 (2017). "분자 집단 유전학". 유전학. 205 (3): 1003–1035. doi : 10.1534 / genetics.116.196493. PMC 5340319. PMID 28270526.
- ^ 할단, J. B. S. (1927). "자연 및 인공 선택의 수학적 이론, 파트 V : 선택과 돌연변이". 케임브리지 철학 사회의 수학적 절차. 23 (7): 838–844. 비코드: 1927PCPS... 23..838H. doi: 10.1017/S0305004100015644.
- ^ Orr, H. A. (2010). "유익한 돌연변이의 집단 유전학". 왕립 학회의 철학적 거래 B : 생물 과학. 365 (1544): 1195–1201. 도이 : 10.1098 / rstb.2009.0282. PMC 2871816. PMID 20308094.
- ^ 허미슨, J.; 페닝스, P. S. (2005). "소프트 스윕 : 서있는 유전 적 변이로부터의 적응의 분자 집단 유전학". 유전학. 169 (4): 2335–2352. doi : 10.1534 / genetics.104.036947. PMC 1449620. PMID 15716498.
- ^ 길레스피, 존 (2004). 인구 유전학 : 간결한 가이드 (2nd ed.). 존스 홉킨스 대학 출판부 ISBN 978-0-8018-8008-7.
- ^ 미코, I. (2008). "Epistasis : 유전자 상호 작용 및 표현형 효과". 자연 교육. 1 (1): 197.
- ^ 버거, D.; Postma, E. (2014년 10월 13일). "감소하는 수익률 에피스타시스에 대한 편향된 추정치? 경험적 증거 재검토". 유전학. 198 (4): 1417–1420. doi : 10.1534 / genetics.114.169870. PMC 4256761. PMID 25313131.
- ^ 쿠요스, 로저 D.; 실란더, 올린 케이; 본회퍼, 세바스찬 (June 2007). "해로운 돌연변이와 재조합의 진화 사이의 에피스타시스". 생태학 및 진화의 동향. 22 (6): 308–315. doi : 10.1016 / j.tree.2007.02.014. PMID 17337087.
- ^ 크로우, J. F. (1997년 8월 5일). "높은 자발적 돌연변이율 : 그것은 건강상의 위험입니까?". 미국 국립 과학 아카데미의 절차. 94 (16): 8380–8386. 비코드:1997PNAS... 94.8380C. doi: 10.1073/pnas.94.16.8380. PMC 33757. PMID 9237985.
- ^ 스미스, N. G. C.; 웹스터, 엠티; 엘르그렌, H. (2002). "인간 게놈의 결정론적 돌연변이율 변이". 게놈 연구. 12 (9): 1350–1356. 도이 : 10.1101 / gr.220502. PMC 186654. PMID 12213772.
- ^ 페트로프, D. A. (2000). "게놈 크기의 결정 인자로서의 DNA 손실에 대한 증거". 과학. 287 (5455): 1060–1062. Bibcode : 2000Sci ... 287.1060P. doi: 10.1126/science.287.5455.1060. ISSN 0036-8075. PMID 10669421.
- ^ 페트로프, D. A. (2002). "초파리에서 게놈 크기의 DNA 손실과 진화". 유전학. 115 (1): 81–91. 도이 : 10.1023 / A : 1016076215168. PMID 12188050. S2CID 5314242.
- ^ 키온트케, 케이.; 바리에르, A.; 콜로투예프, I.; Podbilewicz, B.; 솜머, R.; 피치, 디 에이치; 펠릭스, M. A. (2007). "선충류 외음부 발달의 진화에서 추세, 정체 및 표류". 현재 생물학. 17 (22): 1925–1937. doi : 10.1016 / j.cub.2007.10.061. PMID 18024125. S2CID 4503181.
- ^ 브렌들, C.; 베어, C. F.; 펠릭스, M. A. (2010). 바쉬, 그레고리 S. (ed.). "발달 시스템에서 돌연변이로 접근 가능한 표현형 공간의 편견과 진화". PLOS 유전학. 6 (3): e1000877. doi:10.1371/journal.pgen.1000877. PMC 2837400. PMID 20300655.
- ^ 팔머, RA (2004). "대칭 파괴와 개발의 진화". 과학. 306 (5697): 828–833. Bibcode : 2004Sci ... 306..828P. CiteSeerX 10.1.1.631.4256. doi:10.1126/science.1103707. PMID 15514148. S2CID 32054147.
- ^ 웨스트 에버하르트, M-J. (2003). 발달 가소성과 진화. 뉴욕 : 옥스포드 대학 출판부 ISBN 978-0-19-512235-0.
- ^ 스톨츠퍼스, A.; 얄폴스키, L. Y. (2009). "등반 가능성 : 진화에서 비 무작위성의 원인으로서의 돌연변이". 유전 저널. 100 (5): 637–647. doi:10.1093/jhered/esp048. PMID 19625453.
- ^ 얄폴스키, L. Y.; Stoltzfus, A. (2001). "진화의 지향적 요인으로서의 변이의 도입에 대한 편견". 에볼의 데브. 3 (2): 73–83. doi : 10.1046 / j.1525-142x.2001.003002073.x. PMID 11341676. S2CID 26956345.
- ^ 소여, S. A.; 파르쉬, J.; 장, Z.; 하틀, D. L. (2007). "초파리에서 거의 중립적 인 아미노산 대체물 중 긍정적 인 선택의 유병률". 국립 과학 아카데미의 절차. 104 (16): 6504–6510. doi : 10.1073 / pnas.0701572104. ISSN 0027-8424. PMC 1871816. PMID 17409186.
- ^ 할단, J. B. S. (1933). "진화에서 재발 돌연변이에 의해 연주 된 부분". 미국 자연 주의자. 67 (708): 5–19. 도이 : 10.1086 / 280465. JSTOR 2457127. S2CID 84059440.
- ^ 프로타스, 메레디스; 콘래드, 엠.; 그로스, J. B.; 타빈, C.; 보로 스키, R (2007). "멕시코 동굴 테트라, Astyanax mexicanus에서의 회귀 진화". 현재 생물학. 17 (5): 452–454. doi : 10.1016 / j.cub.2007.01.051. PMC 2570642. PMID 17306543.
- ^ 마우간, 에이치; 마셀, J.; 버키, W. C.; 니콜슨, W. L. (2007). "바실러스 서브틸리스의 실험 집단에서 다공성의 손실에서 돌연변이 축적 및 선택의 역할". 유전학. 177 (2): 937–948. doi : 10.1534 / genetics.107.075663. PMC 2034656. PMID 17720926.
- ^ 마셀, J.; 왕, O. D.; Maughan, H. (2007). "환경 정체의 오랜 기간 동안 적응 가소성의 손실". 미국 자연 주의자. 169 (1): 38–46. 도이 : 10.1086 / 510212. PMC 1766558. PMID 17206583.
- ^ 헤이스팅스, P. J.; 루프스키, J. R.; 로젠버그, S. M.; 이라, G. (2009). "유전자 카피 수의 변화 메커니즘". 자연 리뷰 유전학. 10 (8): 551–564. 도이 : 10.1038 / nrg2593. PMC 2864001. PMID 19597530.
- ^ 엠., 롱; 베트란, E.; 손튼, 케이; 왕, W. (2003년 11월). "새로운 유전자의 기원 : 젊은이와 노인의 엿보기". Nat. Rev. Genet. 4 (11): 865–75. 도이 : 10.1038 / nrg1204. PMID 14634634. S2CID 33999892.
- ^ 리우, 노스캐롤라이나; 오카무라, 케이; 타일러, 디 엠; 필립스; 정; 라이 (2008). "동물 마이크로RNA 유전자의 진화와 기능적 다양화". 세포 연구. 18 (10): 985–996. 도이 : 10.1038 / cr.2008.278. PMC 2712117. PMID 18711447.
- ^ 맥리자흐트, 아오이페; Hurst, Laurence D. (2016년 7월 25일). "de novo 유전자 연구에서 열린 질문 : 무엇을, 어떻게, 왜". 자연 리뷰 유전학. 17 (9): 567–578. 도이 : 10.1038 / nrg.2016.78. PMID 27452112. S2CID 6033249.
- ^ Jump up to:a b 마셀, J. (2011). "유전 적 표류". 현재 생물학. 21 (20): R837–R838. doi : 10.1016 / j.cub.2011.08.007. PMID 22032182.
- ^ 후투이마, 더글러스 (1998). 진화 생물학. 시나우어 어소시에이츠. p. 용어집. ISBN 978-0-87893-189-7.
- ^ 애버스, 샬럿 (1989). 진화의 과정과 패턴. 옥스포드 대학 출판부.
- ^ 월, L. M. (2011). "N과 s가 다를 때 고정 : 고전적인 접근 방식은 우아한 새로운 결과를 제공합니다". 유전학. 188 (4): 783–785. doi : 10.1534 / genetics.111.131748. PMC 3176088. PMID 21828279.
- ^ 바톤, 니콜라스 에이치; 브릭스, 데릭 E. G.; 아이젠, 조나단 A.; 골드스타인, 데이비드 비; Patel, Nipam H. (2007). 진화. 콜드 스프링 하버 실험실 출판사 p. 417. ISBN 978-0-87969-684-9.
- ^ 후투이마, 더글러스 (1998). 진화 생물학. 시나우어 어소시에이츠. 320쪽. ISBN 978-0-87893-189-7.
- ^ 길레스피, J. H. (2000). "무한한 인구의 유전 적 표류 : 의사 히치 하이킹 모델". 유전학. 155 (2): 909–919. doi : 10.1093 / 유전학 / 155.2.909. PMC 1461093. PMID 10835409.
- ^ Provine, William B. The "Random Genetic Drift" Fallacy. 공간을 만듭니다.
- ^ 니허, 리처드 A.; Shraiman, Boris I. (August 2011). "대규모 학부 성 집단에서의 유전 적 초안과 준 중립성". 유전학. 188 (4): 975–996. arXiv : 1108.1635. doi : 10.1534 / genetics.111.128876. ISSN 0016-6731. PMC 3176096. PMID 21625002.
- ^ 부스턴, P. M.; 필킹턴, J. G.; 외. (2007). "광대어들은 가까운 친척들로 구성되어 있는가? Amphiprion percula에서 마이크로 위성 DNA vraiation의 분석". 분자 생태학. 12 (3): 733–742. 도이 : 10.1046 / j.1365-294X.2003.01762.x. PMID 12675828. S2CID 35546810.
- ^ 레파시, V.; 스토우, A. J.; 브리스코, D. A. (2007). "미세 규모의 유전 구조, 공동 창립 및 호주 알로다핀 벌 (Ramphocinclus brachyurus)에서의 다중 교미". 동물학 저널. 270 (4): 687–691. doi : 10.1111 / j.1469-7998.2006.00191.x.
- ^ Jump up to:a b 수, 에이치; Qu, L.-J.; 그, 케이; 장, Z.; 왕, J; 첸, Z.; 구, H. (2003). "중국의 만리장성 : 유전자 흐름에 대한 물리적 장벽?". 유전. 90 (3): 212–219. doi : 10.1038 / sj.hdy.6800237. ISSN 0018-067X. PMID 12634804. S2CID 13367320.
- ^ Gravel, S. (2012). "지역 조상의 인구 유전학 모델". 유전학. 1202 (2): 607–619. arXiv : 1202.4811. Bibcode : 2012arXiv1202.4811G. doi : 10.1534 / genetics.112.139808. PMC 3374321. PMID 22491189.
- ^ 모얀, C.; Rieseberg, L. (2004). "종들이 집단적으로 진화하는 방법 : 유리한 대립 유전자의 확산을위한 유전자 흐름과 선택의 함의". 분자 생태학. 13 (6): 1341–56. 도이 : 10.1111 / j.1365-294X.2004.02164.x. PMC 2600545. PMID 15140081.
- ^ 볼닉, 다니엘 I.; 노실, 패트릭 (2007년 9월). "이주 부하에 종속되는 인구의 자연 선택". 진화. 61 (9): 2229–2243. doi : 10.1111 / j.1558-5646.2007.00179.x. PMID 17767592. S2CID 25685919.
- ^ 부처, 얀; 두아디, 크리스토프 제이; 팍케, 알 테인; 월시, 데이비드 에이; 부드로, 메리 엘렌 알; 네스보, 카밀라 L.; 케이스, 레베카 제이; 두리틀, W. 포드 (2003). "측방 유전자 전달과 원핵 그룹의 기원". 유전학의 연례 검토. 37 (1): 283–328. doi:10.1146/annurev.genet.37.050503.084247. ISSN 0066-4197. PMID 14616063.
- ^ 월시, T. (2006). "다중 저항의 조합 유전 적 진화". 미생물학의 현재 의견. 9 (5): 476–82. 도이 : 10.1016 / j.mib.2006.08.009. PMID 16942901.
- ^ 콘도, 노스캐롤라이나; 니코, 노스캐롤라이나 주; 이지치, 노스캐롤라이나 주; 시마다, 엠.; 후카츠, T. (2002). "Wolbachia endosymbiont의 게놈 단편은 숙주 곤충의 X 염색체로 옮겨졌습니다". 국립 과학 아카데미의 절차. 99 (22): 14280–14285. 비코드:2002PNAS... 9914280K. doi: 10.1073/pnas.222228199. ISSN 0027-8424. PMC 137875. PMID 12386340.
- ^ Sprague, G. (1991). "왕국 간의 유전 적 교환". 유전학 및 개발에 대한 현재 의견. 1 (4): 530–533. 도이 : 10.1016 / S0959-437X (05) 80203-5. PMID 1822285.
- ^ 글래디셰프, E. A.; 메셀슨, 엠.; Arkhipova, I. R. (2008). "Bdelloid Rotifers의 대규모 수평 유전자 전달". 과학. 320 (5880): 1210–1213. 비코드:2008Sci... 320.1210G. doi: 10.1126/science.1156407. ISSN 0036-8075. PMID 18511688. S2CID 11862013.
- ^ 발도, A.; McClure, M. (1999년 9월 1일). "바이러스와 그 숙주에서 dUTPase-코딩 유전자의 진화 및 수평 전달". 바이러스학 저널. 73 (9): 7710–7721. 도이 : 10.1128 / JVI.73.9.7710-7721.1999. PMC 104298. PMID 10438861.
- ^ 풀, A.; 페니, D. (2007). "진핵 생물의 기원에 대한 가설 평가". 바이오에세이. 29 (1): 74–84. doi : 10.1002 / bies.20516. PMID 17187354.
- ^ 와이즈만, 디 비; Hallatschek, O. (2014년 1월 15일). "선형 염색체를 가진 큰 성적 집단에서의 적응 속도". 유전학. 196 (4): 1167–1183. doi : 10.1534 / genetics.113.160705. PMC 3982688. PMID 24429280.
- ^ 와이즈만, 다니엘 비; 바톤, 니콜라스 에이치; McVean, Gil (2012년 6월 7일). "성적 인구의 적응 대체 비율에 대한 제한". PLOS 유전학. 8 (6): e1002740. doi:10.1371/journal.pgen.1002740. PMC 3369949. PMID 22685419.
- ^ Neher, R. A.; 슈라이만, B. I.; 피셔, D. S. (2009년 11월 30일). "대규모 성적 인구의 적응률". 유전학. 184 (2): 467–481. arXiv : 1108.3464. doi : 10.1534 / genetics.109.109009. PMC 2828726. PMID 19948891.
- ^ 데사이, 마이클 엠; 피셔, 다니엘 S. (2007). "유익한 돌연변이 선택 균형과 긍정적 인 선택에 대한 연계의 효과". 유전학. 176 (3): 1759–1798. doi : 10.1534 / genetics.106.067678. PMC 1931526. PMID 17483432.
- ^ Lewontin, R. C. (1973). 진화적 변화의 유전적 기초([4차 인쇄.] ed.). 뉴욕 : 컬럼비아 대학 출판부 ISBN 978-0231033923.
- ^ Jump up to:a b 엘레그렌, 한스; 갈티에, 니콜라스 (2016년 6월 6일). "유전 적 다양성의 결정 요인". 자연 리뷰 유전학. 17 (7): 422–433. 도이 : 10.1038 / nrg.2016.58. PMID 27265362. S2CID 23531428.
- ^ 코르벳-데티그, 러셀 비; 하틀, 다니엘 엘; 삭턴, 티모시 비; Barton, Nick H. (2015년 4월 10일). "자연 선택은 광범위한 종에 걸쳐 중립적 인 다양성을 제한합니다". PLOS 생물학. 13 (4): e1002112. doi:10.1371/journal.pbio.1002112. PMC 4393120. PMID 25859758.
- ^ 성, 더블유; 애커만, 엠에스; 밀러, S. F.; 도크, T. G.; 린치, M. (2012년 10월 17일). "드리프트-장벽 가설과 돌연변이-속도 진화"(PDF). 국립 과학 아카데미의 절차. 109 (45): 18488–18492. 비코드:2012PNAS.. 10918488S. doi: 10.1073/pnas.1216223109. PMC 3494944. PMID 23077252.
- ^ 찰스워스, J. 아이어-워커 (2008). "맥도날드-크라이트만 테스트와 약간 해로운 돌연변이". 분자 생물학과 진화. 25 (6): 1007–1015. 도이 : 10.1093 / molbev / msn005. PMID 18195052.
- ^ Eyre-Walker, A. (2006). "적응 진화의 게놈 속도"(PDF). 생태학과 진화의 동향. 21 (10): 569–575. doi : 10.1016 / j.tree.2006.06.015. PMID 16820244.
- ^ 스미스, N. G. C.; Eyre-Walker, A. (2002). "초파리의 적응 단백질 진화". 자연. 415 (6875): 1022–1024. Bibcode:2002Natur.415.1022S. 도이 : 10.1038 / 4151022a. PMID 11875568. S2CID 4426258.
- ^ 한, M. W. (2008). "분자 진화의 선택 이론을 향해". 진화. 62 (2): 255–265. doi : 10.1111 / j.1558-5646.2007.00308.x. PMID 18302709. S2CID 5986211.
- ^ 프리처드, J. K.; 스티븐스, 엠.; Donnelly, P. (June 2000). "다중유전자좌 유전자형 데이터를 이용한 집단 구조의 추론". 유전학. 155 (2): 945–959. doi : 10.1093 / 유전학 / 155.2.945. ISSN 0016-6731. PMC 1461096. PMID 10835412.
- ^ 진실성, 로버트; 니콜스, 리처드 A. (2016년 8월). "구조화 된 인구에서 하위 인구 수 (K)의 추정". 유전학. 203 (4): 1827–1839. doi : 10.1534 / genetics.115.180992. ISSN 0016-6731. PMC 4981280. PMID 27317680.
- ^ 만릭, 올리버; 샤반느, 델핀; 다니엘, 클레어; 베이더, 라스; 알렌, 사이먼 제이; 셔윈, 윌리엄 B. (2018년 11월 13일). "인구 통계학과 유전학은 돌고래 근원 싱크 역학의 반전을 제안하며, 보존에 대한 함의를 가지고 있습니다." 해양 포유류 과학. 35 (3): 732–759. doi : 10.1111 / mms.12555. S2CID 92108810.
- ^ 구텐쿤스트, 라이언 N.; 에르난데스, 라이언 디; 윌리엄슨, 스콧 에이치; 부스타만테, 카를로스 D.; McVean, Gil (2009년 10월 23일). "다차원 SNP 주파수 데이터로부터 여러 집단의 공동 인구 통계 학적 역사를 추론". PLOS 유전학. 5 (10): e1000695. arXiv : 0909.0925. doi:10.1371/journal.pgen.1000695. PMC 2760211. PMID 19851460.
- ^ 스니고프스키, P. (2000). 게리쉬 피; 존슨 T;. 면도기 A. "돌연변이 속도의 진화 : 결과와 원인을 분리". 바이오에세이. 22 (12): 1057–1066. doi : 10.1002 / 1521-1878 (200012)22 : 12<1057 : : AID-BIES3 >3.0.CO; 2-W. PMID 11084621. S2CID 36771934.
- ^ 린치, 마이클; 코너리, 존 S. (2003). "게놈 복잡성의 기원". 과학. 302 (5649): 1401–1404. Bibcode : 2003Sci ... 302.1401L. CiteSeerX 10.1.1.135.974. doi:10.1126/science.1089370. PMID 14631042. S2CID 11246091.
- ^ 라존, E.; 마셀, J. (2011년 1월 3일). "분자 오류율의 진화와 진화에 대한 결과". 국립 과학 아카데미의 절차. 108 (3): 1082–1087. 비코드:2011PNAS.. 108.1082R. doi: 10.1073/pnas.1012918108. PMC 3024668. PMID 21199946.
외부 링크[편집]

'생명공학' 카테고리의 다른 글
| Cytogenomics- 세포유전체학 (0) | 2022.10.04 |
|---|---|
| Akademie der Wissenschaften zu Göttingen -Bioökonomie (0) | 2022.10.02 |
| 진화 역학 (0) | 2022.09.21 |
| 고세균Archaebacteria (0) | 2022.09.21 |
| 생명 (0) | 2022.09.21 |





