에우클레이데스의 원론

《유클리드의 원론》(그리스어: Στοιχεῖα, 스토이케이아)은 고대 그리스의 저명한 수학자인 에우클레이데스(유클리드)가 기원전 3세기에 집필한 책으로 총 13권으로 구성되어 있다. 그리스어 제목 Στοιχεῖα는 ‘원소’, ‘구성 요소’, ‘글자’ 등을 뜻하는 단어이며, 기하학 원본이라는 제목으로도 불리며, 흔히 ‘세계 최초의 수학 교과서’로 일컬어진다. 에우클레이데스는 이 책에서 정의 131개와 공준 5개, 공리 5개로부터 465개의 명제를 만들어냈다.
목차
- 1 주요 내용
- 2 유클리드 원론 제2권 법칙4
- 3 제1권 법칙47
- 4 2권 법칙 12
- 5 2권 법칙13
- 6 3권 법칙 3
- 7 2권 법칙 9
- 8 2권 법칙 8
- 9 2권 법칙 5와 6
- 10 같이 보기
- 11 참고 자료
- 12 외부 링크
주요 내용[편집]
《원론》의 내용은 다음과 같다. 제 1권에서 제 4권까지는 2차원 기하학에 관한 내용을 담고 있다.
- 제1권 : 필수적이고 예비적인 정의와 설명 및 공준과 공리로 시작한다.[1] 제1권의 정리 중에는 합동, 평행선, 직선으로 이루어진 도형 등에 관한 친숙한 정리들이 포함되어 있다. 그 책의 마지막 두 정리인 정리 47과 48은 피타고라스 정리와 그 역이다. 18세기까지 기하학 교과서로 쓰인 이유도 여기에 있다. : 겨우 14개의 정리만을 포함하고 있는 작은 책인데 여기에서는 주로 피타고라스 학파의 기하 대수학을 다루고 있다. 이 책의 정리 12와 13은 근본적으로 오늘날 코사인 법칙으로 알려진 피타고라스 정리의 일반화이다.
- 제3권 : 39개의 정리로 이루어졌으며, 원, 현, 할선, 접선, 연관된 각도의 측정 등에 관한 정리들을 포함하고 있다.
- 제4권 : 16개의 정리로 이루어져 있으며 자와 컴퍼스를 이용한 작도, 주어진 원에 내접하는 경우와 외접하는 경우의 작도, 정다각형의 작도를 포함하고 있다.
제 5권부터 비율과 비례로부터 시작해 기초적인 수론을 다룬다. 제 6권에서는 제 4권에 이어 이를 도형에 적용하고 제 10권까지 다시 수론을 다룬다.
- 제5권 : 에우독소스의 비율 이론에 대한 대가다운 설명에 충당했다. 이 책은 수학적인 문헌 중에서 가장 훌륭한 걸작 중의 하나로 간주된다.
- 제6권 : 에우독소스의 이론을 닮음 도형의 연구에 응용하고 있다.
- 제7권 : 두 개 이상의 정수에 대한 최대공약수를 구하는 방법(유클리드 호제법)으로 시작된다. 또한 초기 피타고라스 학파의 비율 이론에 대한 설명을 발견할 수 있다.
- 제8권 : 주로 연비례와 그것과 관련된 등비수열을 다루고 있다. 만약 a : b = c: d가 성립하면 a, b, c, d는 등비수열을 형성한다.
- 제9권 : 수론에서 중요한 많은 정리들이 있는데 먼저 정리14는 중요한 ‘산술의 기본 정리(Fundamental theorem of arithmetic)’즉 “1보다 큰 임의의 정수는 반드시 소수들의 곱으로 표현될 수 있으며 근본적으로 단 한가지 방법으로 표현된다.”는 정리와 동치이다. 정리 20에서 ‘소수의 개수는 무한하다.’는 사실에 대한 매우 세련된 증명을 찾아볼 수 있다. 정리 35는 등비수열의 첫 n개의 항의 합에 대한 공식을 기하적으로 유도했다. 그리고 이 책의 마지막 정리인 정리 36은 짝수인 완전수를 만드는 놀라운 공식을 증명하고 있다.
- 제10권 : 무리수들, 즉 어떤 주어진 선분의 길이를 단위로 재어 비율로 나타낼 수 없는 길이를 다루고 있다.
제 11권에서 제 13권까지는 3차원 기하학에 관한 내용들 담고 있다.
- 제11권 : 선과 면·면과 면·평행육면체·정육면체·각기둥
- 제12권 : 원의 면적과 각뿔·각기둥·원뿔·원기둥·구의 체적(단, 원주율은 쓰지 않음. 원의 면적은 지름의 제곱에 비례하고 구의 체적은 지름의 세제곱에 비례함을 이용)
- 제13권 : 정사면체, 정육면체, 정팔면체, 정십이면체, 정이십면체의 다섯 종류만이 정다면체임을 증명함.
유클리드 원론 제2권 법칙4[편집]
|
|
| A B ¯ {\displaystyle \;{\overline {AB}}} 에서 임의의 한 점 C {\displaystyle C} 에대해서 C B ¯ = B I ¯ = A H ¯ {\displaystyle {\overline {CB}}={\overline {BI}}={\overline {AH}}} 이고,[2]A B ¯ = B D ¯ = E D ¯ {\displaystyle {\overline {AB}}={\overline {BD}}={\overline {ED}}} 이므로,A C ¯ = E F ¯ = E H ¯ {\displaystyle {\overline {AC}}={\overline {EF}}={\overline {EH}}} A B ¯ 2 = A C ¯ 2 + B C ¯ 2 + 2 ( A C ¯ ⋅ B C ¯ ) {\displaystyle {\overline {AB}}^{2}={\overline {AC}}^{2}+{\overline {BC}}^{2}+2\left({\overline {AC}}\cdot {\overline {BC}}\right)}
따라서, A C ¯ = H E ¯ = a {\displaystyle {\overline {AC}}={\overline {HE}}=a} C B ¯ = A H ¯ = b {\displaystyle {\overline {CB}}={\overline {AH}}=b} A C ¯ + C B ¯ = A B ¯ = A E ¯ = c {\displaystyle {\overline {AC}}+{\overline {CB}}={\overline {AB}}={\overline {AE}}=c} 일때,( a + b ) 2 = a 2 + 2 a b + b 2 {\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}} c 2 = a 2 + 2 a b + b 2 {\displaystyle c^{2}=a^{2}+2ab+b^{2}}이것은 대표적인 곱셈공식이다. |
제1권 법칙47[편집]
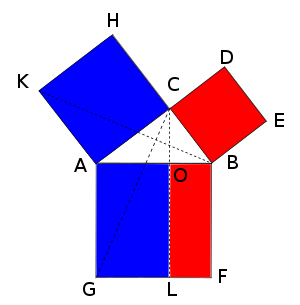
A C ¯ 2 = A O ¯ ⋅ A G ¯ , B C ¯ 2 = O B ¯ ⋅ B F ¯ {\displaystyle {\overline {AC}}^{2}={\overline {AO}}\cdot {\overline {AG}}\qquad ,\qquad {\overline {BC}}^{2}={\overline {OB}}\cdot {\overline {BF}}}
A C ¯ 2 + B C ¯ 2 = ( A O ¯ ⋅ A G ¯ ) + ( O B ¯ ⋅ B F ¯ ) {\displaystyle {\overline {AC}}^{2}+{\overline {BC}}^{2}=\left({\overline {AO}}\cdot {\overline {AG}}\right)+\left({\overline {OB}}\cdot {\overline {BF}}\right)}
A C ¯ 2 + B C ¯ 2 = A B ¯ 2 {\displaystyle {\overline {AC}}^{2}+{\overline {BC}}^{2}={\overline {AB}}^{2}}
유클리드의 피타고라스 정리 증명은 닮음꼴 이론을 사용하지 않으므로서 순수하게 기하학적이다.[3]
A C ¯ = b . B C ¯ = a , A B ¯ = c {\displaystyle {\overline {AC}}=b\;\;.\;\;{\overline {BC}}=a\;\;,\;\;{\overline {AB}}=c}
일때,b 2 + a 2 = c 2 {\displaystyle b^{2}+a^{2}=c^{2}}
2권 법칙 12[편집]
|
|
|
유클리드 원론 2권 법칙4 에서, 둔각삼각형 △ A B C {\displaystyle \triangle {ABC}} 에서, B D ¯ {\displaystyle ,\;{\overline {BD}}} 의 임의의 한점 C {\displaystyle C} 에대해서,[4] B D ¯ 2 = B C ¯ 2 + C D ¯ 2 + 2 ( B C ¯ ⋅ C D ¯ ) {\displaystyle {\overline {BD}}^{2}={\overline {BC}}^{2}+{\overline {CD}}^{2}+2\left({\overline {BC}}\cdot {\overline {CD}}\right)} A B ¯ 2 = B D ¯ 2 + A D ¯ 2 {\displaystyle {\overline {AB}}^{2}={\overline {BD}}^{2}+{\overline {AD}}^{2}\;\;}그리고, A C ¯ 2 = C D ¯ 2 + A D ¯ 2 {\displaystyle {\overline {AC}}^{2}={\overline {CD}}^{2}+{\overline {AD}}^{2}\;\;} A C ¯ 2 − C D ¯ 2 = A D ¯ 2 {\displaystyle {\overline {AC}}^{2}-{\overline {CD}}^{2}={\overline {AD}}^{2}\;\;}따라서, A B ¯ 2 = B D ¯ 2 + A D ¯ 2 {\displaystyle {\overline {AB}}^{2}={\overline {BD}}^{2}+{\overline {AD}}^{2}} A B ¯ 2 = ( B C ¯ 2 + C D ¯ 2 + 2 ( B C ¯ ⋅ C D ¯ ) ) + ( A C ¯ 2 − C D ¯ 2 ) {\displaystyle {\overline {AB}}^{2}=\left({\overline {BC}}^{2}+{\overline {CD}}^{2}+2\left({\overline {BC}}\cdot {\overline {CD}}\right)\right)+\left({\overline {AC}}^{2}-{\overline {CD}}^{2}\right)} A B ¯ 2 = B C ¯ 2 + A C ¯ 2 + 2 ( B C ¯ ⋅ C D ¯ ) {\displaystyle {\overline {AB}}^{2}={\overline {BC}}^{2}+{\overline {AC}}^{2}+2\left({\overline {BC}}\cdot {\overline {CD}}\right)} |
그리고
|
|
| c o s ( π − α ) = C D ¯ A C ¯ {\displaystyle cos(\pi -\alpha )={{\overline {CD}} \over {\overline {AC}}}} C D ¯ = A C ¯ cos ( π − α ) {\displaystyle {\overline {CD}}={\overline {AC}}\cos(\pi -\alpha )} C D ¯ = − A C ¯ cos α {\displaystyle {\overline {CD}}=-{\overline {AC}}\cos \alpha }
따라서, A B ¯ 2 = B C ¯ 2 + A C ¯ 2 + 2 ( B C ¯ ⋅ C D ¯ ) {\displaystyle {\overline {AB}}^{2}={\overline {BC}}^{2}+{\overline {AC}}^{2}+2\left({\overline {BC}}\cdot {\overline {CD}}\right)} A B ¯ 2 = B C ¯ 2 + A C ¯ 2 − 2 ( B C ¯ ⋅ A C ¯ cos α ) {\displaystyle {\overline {AB}}^{2}={\overline {BC}}^{2}+{\overline {AC}}^{2}-2\left({\overline {BC}}\cdot {{\overline {AC}}\cos \alpha }\right)} c 2 = a 2 + b 2 − 2 a b cos α {\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos \alpha } |
이것은 제2코사인법칙이 되겠다.
2권 법칙13[편집]
|
|
|
예각삼각형을 예약하고,[5] 이것을 c o s i n e {\displaystyle cosine} 에대해 나타내보면, B C ¯ = B D ¯ + D C ¯ {\displaystyle {\overline {BC}}={\overline {BD}}+{\overline {DC}}} cos B = B D ¯ c {\displaystyle \cos B={{\overline {BD}} \over {c}}} cos B c = B D ¯ {\displaystyle \cos Bc={\overline {BD}}} cos C = D C ¯ b {\displaystyle \cos C={{\overline {DC}} \over {b}}} cos C b = D C ¯ {\displaystyle \cos Cb={\overline {DC}}}따라서, B C ¯ = B D ¯ + D C ¯ {\displaystyle {\overline {BC}}={\overline {BD}}+{\overline {DC}}} a = c cos B + b cos C {\displaystyle a=c\cos B+b\cos C}이것은,코사인법칙의 제1코사인법칙이다. a = b cos C + c cos B , b = c cos A + a cos C , c = a cos B + b cos A {\displaystyle a=b\cos C+c\cos B,b=c\cos A+a\cos C,c=a\cos B+b\cos A} |
3권 법칙 3[편집]
|
|
|
원과 그 원의 중심점에 한점을 두는 삼각형을 예약하고,[6] 두 점 사이의 거리에서,l = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 {\displaystyle l={\sqrt {({x_{2}}-{x_{1}})^{2}+({y_{2}}-{y_{1}})^{2}}}} 이므로,D = ( cos α , sin α ) , C = ( cos β , sin β ) {\displaystyle D=(\cos \;\alpha ,\sin \;\alpha )\;\;,\;\;C=(\cos \beta ,\sin \beta )} D C ¯ 2 = ( cos β − cos α ) 2 + ( sin β − sin α ) 2 {\displaystyle {\overline {DC}}^{2}=(\cos \beta -\cos \;\alpha )^{2}+(\sin \beta -\sin \;\alpha )^{2}} = ( ( cos β − cos α ) ⋅ ( cos β − cos α ) ) + ( ( sin β − sin α ) ⋅ ( − sin β − sin α ) ) {\displaystyle =\left((\cos \beta -\cos \;\alpha )\cdot (\cos \beta -\cos \;\alpha )\right)+\left((\sin \beta -\sin \;\alpha )\cdot (-\sin \beta -\sin \;\alpha )\right)} = ( ( cos β ) 2 − 2 cos α cos β + ( cos α ) 2 ) + ( ( sin β ) 2 − 2 sin α sin β + ( sin α ) 2 ) {\displaystyle =\left((\cos \beta )^{2}-2\cos \alpha \cos \beta +(\cos \;\alpha )^{2}\right)+\left((\sin \beta )^{2}-2\sin \alpha \sin \beta +(\sin \alpha )^{2}\right)} = ( cos β ) 2 + ( cos α ) 2 + ( sin β ) 2 + ( sin α ) 2 − 2 cos α cos β − 2 sin α sin β {\displaystyle =(\cos \beta )^{2}+(\cos \;\alpha )^{2}+(\sin \beta )^{2}+(\sin \alpha )^{2}-2\cos \alpha \cos \beta -2\sin \alpha \sin \beta } = ( cos 2 β + cos α 2 ) + ( sin 2 β + sin 2 α ) − 2 ( cos α cos β + sin α sin β ) {\displaystyle =(\cos ^{2}\beta +\cos \;\alpha ^{2})+(\sin ^{2}\beta +\sin ^{2}\alpha )-2\left(\cos \alpha \cos \beta +\sin \alpha \sin \beta \right)} sin 2 x + cos 2 x = 1 {\displaystyle \sin ^{2}{x}+\cos ^{2}{x}=1}따라서, = 1 + 1 − 2 ( cos α cos β + sin α sin β ) {\displaystyle =1+1-2\left(\cos \alpha \cos \beta +\sin \alpha \sin \beta \right)} D C ¯ 2 = 2 − 2 ( cos α cos β + sin α sin β ) {\displaystyle {\overline {DC}}^{2}=2-2\left(\cos \alpha \cos \beta +\sin \alpha \sin \beta \right)} |
한편,
이것은,제2코사인법칙에서는,D C ¯ 2 = O D ¯ 2 + O C ¯ 2 − 2 ( O D ¯ ⋅ O C ¯ cos ( α − β ) ) {\displaystyle {\overline {DC}}^{2}={\overline {OD}}^{2}+{\overline {OC}}^{2}-2\left({\overline {OD}}\cdot {{\overline {OC}}\cos(\alpha -\beta )}\right)}
D C ¯ 2 = 1 2 + 1 2 − 2 ( 1 ⋅ 1 cos ( α − β ) ) {\displaystyle {\overline {DC}}^{2}=1^{2}+1^{2}-2\left(1\cdot {1\cos(\alpha -\beta }\right))}
D C ¯ 2 = 2 − 2 cos ( α − β ) {\displaystyle {\overline {DC}}^{2}=2-2\cos \left({\alpha -\beta }\right)}
그리고,
D C ¯ 2 = 2 − 2 cos ( α − β ) = 2 − 2 ( cos α cos β + sin α sin β ) {\displaystyle {\overline {DC}}^{2}=2-2\cos \left({\alpha -\beta }\right)=2-2\left(\cos \alpha \cos \beta +\sin \alpha \sin \beta \right)}
따라서,
cos ( α − β ) = ( cos α cos β + sin α sin β ) {\displaystyle \cos \left({\alpha -\beta }\right)=\left(\cos \alpha \cos \beta +\sin \alpha \sin \beta \right)}
이렇게 삼각함수의 덧셈정리중 코사인함수에 접근해볼수있다.
2권 법칙 9[편집]
|
|
| 정삼각형에서 A E ¯ = 1 {\displaystyle {\overline {AE}}=1} 을 예약하고,[7]A F ¯ 1 = cos α {\displaystyle {{\overline {AF}} \over {1}}={\cos \alpha }} E F ¯ 1 = sin α {\displaystyle {{\overline {EF}} \over {1}}={\sin \alpha }} F D ¯ A F = sin β {\displaystyle {{\overline {FD}} \over {AF}}={\sin \beta }} s i n a {\displaystyle sina} E G ¯ E F ¯ = cos β {\displaystyle {{\overline {EG}} \over {\overline {EF}}}={\cos \beta }} E G ¯ = cos β E F ¯ = cos β sin α {\displaystyle {\overline {EG}}={\cos \beta }{\overline {EF}}={\cos \beta }\,{\sin \alpha }} sin ( α + β ) = E G ¯ + G C ¯ 1 {\displaystyle {\sin(\alpha +\beta )}={{{\overline {EG}}+{\overline {GC}}} \over {1}}} sin ( α + β ) = cos β sin α + sin β cos α {\displaystyle {\sin(\alpha +\beta )}={{\cos \beta }\,{\sin \alpha }}+{\sin \beta \cos \alpha }}
이것은 삼각함수의 덧셈정리중 사인함수이다. 한편,예약된 정삼각형에서,[8]A E ¯ = 1 , ∠ A = ∠ E = ∠ B , ∠ A = ∠ α + ∠ β , ∠ α = ∠ β {\displaystyle {\overline {AE}}=1,\angle A=\angle E=\angle B,\angle A=\angle \alpha +\angle \beta ,\angle \alpha =\angle \beta } E F ¯ 1 = sin α {\displaystyle {{\overline {EF}} \over {1}}={\sin \alpha }} A F ¯ 1 = cos α {\displaystyle {{\overline {AF}} \over {1}}={\cos \alpha }} A D ¯ A F = cos β {\displaystyle {{\overline {AD}} \over {AF}}={\cos \beta }} A D ¯ = cos β A F ¯ {\displaystyle {\overline {AD}}={\cos \beta }{\overline {AF}}} A D ¯ = cos β cos α {\displaystyle {\overline {AD}}={\cos \beta }\,{\cos \alpha }} G F ¯ E F ¯ = sin β {\displaystyle {{\overline {GF}} \over {\overline {EF}}}={\sin \beta }} G F ¯ = sin β E F ¯ {\displaystyle {\overline {GF}}={\sin \beta }{\overline {EF}}} G F ¯ = sin β sin α {\displaystyle {\overline {GF}}={\sin \beta }\,{\sin \alpha }}G F ¯ = C D ¯ = sin β sin α {\displaystyle {\overline {GF}}={\overline {CD}}={\sin \beta }\,{\sin \alpha }} cos ( α + β ) = A C ¯ 1 {\displaystyle {\cos(\alpha +\beta )}={{\overline {AC}} \over {1}}} cos ( α + β ) = A D ¯ − C D ¯ {\displaystyle {\cos(\alpha +\beta )}={{\overline {AD}}-{\overline {CD}}}} cos ( α + β ) = cos β cos α − sin β sin α {\displaystyle {\cos(\alpha +\beta )}={\cos \beta \cos \alpha }-{\sin \beta \sin \alpha }} 이것은 삼각함수의 덧셈정리중 코사인함수이다. |
2권 법칙 8[편집]
|
|
|
기하학에서, 두 점 사이의 거리는 좌표평면에서 임의의 두 점 D ( x 1 , y 1 ) , K ( x 2 , y 2 ) {\displaystyle D(x_{1},y_{1}),K(x_{2},y_{2})} 을 예약하고,[9] 점 D ( x 1 , y 1 ) {\displaystyle D(x_{1},y_{1})} 에서 x {\displaystyle x} 축에 평행하게 그은 직선과 점 K ( x 2 , y 2 ) {\displaystyle K(x_{2},y_{2})} 에서 y {\displaystyle y} 축에 평행하게 그은 직선이 서로 만나는 점 N {\displaystyle N} 을 예약할 수 있다.두 점 D , K {\displaystyle D,K} 사이의 거리를 l {\displaystyle l} 이라고 가정했을때,△ N D K {\displaystyle \triangle NDK} 는 l {\displaystyle l} 을 빗변으로 하는 직각삼각형이고, N K ¯ = x 2 − x 1 , N D ¯ = y 2 − y 1 {\displaystyle {\overline {NK}}=x_{2}-x_{1}\;,\;{\overline {ND}}=y_{2}-y_{1}} 이므로,l , N D ¯ , N K ¯ {\displaystyle l,{\overline {ND}},{\overline {NK}}} 은 피타고라스 정리에 의해 다음과 같은 관계가 있다.l 2 = N K ¯ 2 + N D ¯ 2 = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 {\displaystyle {\begin{aligned}l^{2}&={\overline {NK}}^{2}+{\overline {ND}}^{2}\\&=(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}\end{aligned}}} ⇔ l = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 {\displaystyle \Leftrightarrow l={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}}따라서, 좌표평면에서 두 점 D ( x 1 , y 1 ) , K ( x 2 , y 2 ) {\displaystyle D(x_{1},y_{1}),K(x_{2},y_{2})} 가 있을 때 두 점 사이의 거리 l {\displaystyle l} 은 다음과 같다.l = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 {\displaystyle l={\sqrt {({x_{2}}-{x_{1}})^{2}+({y_{2}}-{y_{1}})^{2}}}} |
2권 법칙 5와 6[편집]
|
|
|
임의의 선분 A B ¯ {\displaystyle {\overline {AB}}} 을 예약하고, A B ¯ {\displaystyle {\overline {AB}}} 을 이등분하는 점 C {\displaystyle C} 를 가정하면,[10]A D ¯ = A C ¯ + C D ¯ = C D ¯ + C B ¯ {\displaystyle {\overline {AD}}={\overline {AC}}+{\overline {CD}}={\overline {CD}}+{\overline {CB}}} B D ¯ = C D ¯ − C B ¯ {\displaystyle {\overline {BD}}=\qquad \qquad \qquad {\overline {CD}}-{\overline {CB}}} A D ¯ ⋅ B D ¯ = ( C D ¯ + C B ¯ ) ( C D ¯ − C B ¯ ) = C D ¯ 2 − C B ¯ 2 {\displaystyle {\overline {AD}}\cdot {\overline {BD}}=\left({\overline {CD}}+{\overline {CB}}\right)\left({\overline {CD}}-{\overline {CB}}\right)={\overline {CD}}^{2}-{\overline {CB}}^{2}} A D ¯ ⋅ B D ¯ + C B ¯ 2 = C D ¯ 2 {\displaystyle {\overline {AD}}\cdot {\overline {BD}}+{\overline {CB}}^{2}={\overline {CD}}^{2}} |
피타고라스 정리의 변형[편집]
A D ¯ ⋅ B D ¯ + C B ¯ 2 = C D ¯ 2 {\displaystyle {\overline {AD}}\cdot {\overline {BD}}+{\overline {CB}}^{2}={\overline {CD}}^{2}}
( 2 C B ¯ + B D ¯ ) ⋅ B D ¯ + C B ¯ 2 = C D ¯ 2 {\displaystyle \left(2{\overline {CB}}+{\overline {BD}}\right)\cdot {\overline {BD}}+{\overline {CB}}^{2}={\overline {CD}}^{2}}
C D ¯ 2 + C D ¯ 2 = F H ¯ 2 {\displaystyle {\overline {CD}}^{2}+{\overline {CD}}^{2}={\overline {FH}}^{2}}
( 2 C B ¯ + B D ¯ ) ⋅ B D ¯ + C B ¯ 2 + C D ¯ 2 + C D ¯ 2 = C D ¯ 2 + F H ¯ 2 {\displaystyle \left(2{\overline {CB}}+{\overline {BD}}\right)\cdot {\overline {BD}}+{\overline {CB}}^{2}+{\overline {CD}}^{2}+{\overline {CD}}^{2}={\overline {CD}}^{2}+{\overline {FH}}^{2}}
( 2 C B ¯ + B D ¯ ) ⋅ B D ¯ + C B ¯ 2 + C D ¯ 2 = C D ¯ 2 − C D ¯ 2 + F H ¯ 2 {\displaystyle \left(2{\overline {CB}}+{\overline {BD}}\right)\cdot {\overline {BD}}+{\overline {CB}}^{2}+{\overline {CD}}^{2}={\overline {CD}}^{2}-{\overline {CD}}^{2}+{\overline {FH}}^{2}}
( 2 C B ¯ + B D ¯ ) ⋅ B D ¯ + C B ¯ 2 + C D ¯ 2 = F H ¯ 2 {\displaystyle \left(2{\overline {CB}}+{\overline {BD}}\right)\cdot {\overline {BD}}+{\overline {CB}}^{2}+{\overline {CD}}^{2}={\overline {FH}}^{2}}
( 2 C B ¯ ⋅ B D ¯ ) + B D ¯ 2 + C B ¯ 2 + C D ¯ 2 = F H ¯ 2 {\displaystyle \left(2{\overline {CB}}\cdot {\overline {BD}}\right)+{\overline {BD}}^{2}+{\overline {CB}}^{2}+{\overline {CD}}^{2}={\overline {FH}}^{2}}
( ( 2 C B ¯ ⋅ B D ¯ ) + B D ¯ 2 + C B ¯ 2 ) + C D ¯ 2 = F H ¯ 2 {\displaystyle \left(\left(2{\overline {CB}}\cdot {\overline {BD}}\right)+{\overline {BD}}^{2}+{\overline {CB}}^{2}\right)+{\overline {CD}}^{2}={\overline {FH}}^{2}}
그리고,C D ¯ 2 + C D ¯ 2 = F H ¯ 2 {\displaystyle {\overline {CD}}^{2}+{\overline {CD}}^{2}={\overline {FH}}^{2}}
이므로,
C D ¯ 2 = ( ( 2 C B ¯ ⋅ B D ¯ ) + B D ¯ 2 + C B ¯ 2 ) {\displaystyle {\overline {CD}}^{2}=\left(\left(2{\overline {CB}}\cdot {\overline {BD}}\right)+{\overline {BD}}^{2}+{\overline {CB}}^{2}\right)}
이고,( ( 2 C B ¯ ⋅ B D ¯ ) + B D ¯ 2 + C B ¯ 2 ) + ( ( 2 C B ¯ ⋅ B D ¯ ) + B D ¯ 2 + C B ¯ 2 ) = F H ¯ 2 {\displaystyle \left(\left(2{\overline {CB}}\cdot {\overline {BD}}\right)+{\overline {BD}}^{2}+{\overline {CB}}^{2}\right)+\left(\left(2{\overline {CB}}\cdot {\overline {BD}}\right)+{\overline {BD}}^{2}+{\overline {CB}}^{2}\right)={\overline {FH}}^{2}}
피타고라스 정리 응용[편집]
C B ¯ = C D ¯ − D B ¯ {\displaystyle {\overline {CB}}={\overline {CD}}-{\overline {DB}}}
( C B ¯ ) 2 = ( C D ¯ − D B ¯ ) 2 {\displaystyle \left({\overline {CB}}\right)^{2}=\left({\overline {CD}}-{\overline {DB}}\right)^{2}}
C B ¯ 2 = C D ¯ 2 − 2 C D ¯ D B ¯ + D B ¯ 2 {\displaystyle {\overline {CB}}^{2}={\overline {CD}}^{2}-2{\overline {CD}}{\overline {DB}}+{\overline {DB}}^{2}}
C B ¯ 2 + 2 C D ¯ D B ¯ = C D ¯ 2 + D B ¯ 2 {\displaystyle {\overline {CB}}^{2}+2{\overline {CD}}{\overline {DB}}={\overline {CD}}^{2}+{\overline {DB}}^{2}}
D B ¯ = D H ¯ = M H ¯ {\displaystyle {\overline {DB}}={\overline {DH}}={\overline {MH}}}
C H ¯ 2 = C D ¯ 2 + D B ¯ 2 {\displaystyle {\overline {CH}}^{2}={\overline {CD}}^{2}+{\overline {DB}}^{2}}
이고,C B ¯ 2 + 2 C D ¯ D B ¯ = C H ¯ 2 {\displaystyle {\overline {CB}}^{2}+2{\overline {CD}}{\overline {DB}}={\overline {CH}}^{2}}
같이 보기[편집]
참고 자료[편집]
| 위키문헌에 이 글과 관련된 원문이 있습니다. |
| 위키문헌에 이 글과 관련된 원문이 있습니다. |
| 위키미디어 공용에 관련된 미디어 분류가 있습니다. |
- ↑ 오늘날의 수학자들은 ‘공리’와 ‘공준’이라는 단어를 형식논리학의 토대에서 사실상 동의어로 사용하지만, 고대 그리스의 에우클레이데스는 그 두 단어를 채택하는 데 공리는 모든 학문 분야에 공통인 초기 가정인 반면에 공준은 특수한 분야에 한정되는 것이라는 점에서 차이를 두었다고 여겨진다.
- ↑ (유클리드 기하학 원론 2권 법칙4 )http://www.gutenberg.org/files/21076/21076-pdf.pdf?session_id=9bfd9ef535a37ac859a6028f101fa4451e3226cc (구텐베르크 프로젝트,John Casey,퍼블릭 도메인)
- ↑ (구텐베르크 프로젝트-기하학 원론 1권47,John Casey,퍼블릭 도메인)https://www.gutenberg.org/files/21076/21076-pdf.pdf?session_id=b505fb05308448caad895d905f0943ad1eb1f613 page53
- ↑ (유클리드 기하학 원론 2권 법칙12 )http://www.gutenberg.org/files/21076/21076-pdf.pdf?session_id=9bfd9ef535a37ac859a6028f101fa4451e3226cc (구텐베르크 프로젝트,John Casey,퍼블릭 도메인)
- ↑ (유클리드 기하학 원론 2권 법칙13 )http://www.gutenberg.org/files/21076/21076-pdf.pdf?session_id=9bfd9ef535a37ac859a6028f101fa4451e3226cc (구텐베르크 프로젝트,John Casey,Public Domain)
- ↑ (유클리드 기하학 원론 3권 법칙3 )http://www.gutenberg.org/files/21076/21076-pdf.pdf?session_id=9bfd9ef535a37ac859a6028f101fa4451e3226cc (구텐베르크 프로젝트,John Casey,PublicDomain)
- ↑ (유클리드 기하학 원론 2권 법칙9 )http://www.gutenberg.org/files/21076/21076-pdf.pdf?session_id=9bfd9ef535a37ac859a6028f101fa4451e3226cc (구텐베르크 프로젝트,John Casey,Public Domain)
- ↑ (유클리드 기하학 원론 2권 법칙9 )http://www.gutenberg.org/files/21076/21076-pdf.pdf?session_id=9bfd9ef535a37ac859a6028f101fa4451e3226cc (구텐베르크 프로젝트,John Casey,Public Domain)
- ↑ (유클리드 기하학원론 2권 법칙8) http://www.gutenberg.org/files/21076/21076-pdf.pdf?session_id=9bfd9ef535a37ac859a6028f101fa4451e3226cc (구텐베르크 프로젝트)
- ↑ (유클리드 기하학원론 2권 법칙5및6) http://www.gutenberg.org/files/21076/21076-pdf.pdf?session_id=9bfd9ef535a37ac859a6028f101fa4451e3226cc (구텐베르크 프로젝트)
- 기하학 원론 가~자, 이무현 번역, 1997, 교우사.
- "David Joyce Home Page"-"Euclid's Elements"
- 유클리드의 기하학 원론(무료 다운로드, 코이네 그리스어)
- 구텐베르크 프로젝트-유클리드 기하학 원론,1885,John Casey(무료 다운로드,영문)
외부 링크[편집]
- Euclid's Elements (영어) (유클리드의 원론 1~13 권 속의 정의, 공준, 공리, 명제의 내용과 그에 대한 설명, 그리고 명제의 증명)
<img src="//ko.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1x1" alt="" title="" width="1" height="1" style="border: none; position: absolute;" />
원본 주소 "https://ko.wikipedia.org/w/index.php?title=에우클레이데스의_원론&oldid=28674193"
분류:
Στοιχεῖα
'세상만사' 카테고리의 다른 글
| 내고향 전남광산군(광산구) (0) | 2021.02.12 |
|---|---|
| Pythagorean theorem (0) | 2021.02.04 |
| Principia (0) | 2021.02.04 |
| Merriam-Webster’s Word of the Year 2020 (0) | 2021.01.24 |
| Happiness Conference (0) | 2020.12.24 |






























