Strong Emergence Arising from Weak Emergence
Predictions of emergent phenomena, appearing on the macroscopic layer of a complex system, can fail if they are made by a microscopic model. This study demonstrates and analyses this claim on a well-known complex system, Conway’s Game of Life. Straightfo
www.hindawi.com
약한 출현에서 발생하는 강한 출현
추상적인
복잡한 시스템의 거시적 층에 나타나는 창발 현상에 대한 예측은 미시적 모델을 사용하면 실패할 수 있습니다. 본 연구는 잘 알려진 복잡한 시스템인 Conway's Game of Life에 대한 이러한 주장을 입증하고 분석합니다. 간단한 거시적 평균 필드 모델은 사후 방식으로 시뮬레이션 데이터에 적용된 후 이러한 창발 특성을 쉽게 예측할 수 있습니다. 따라서 이러한 예측은 거시 대 거시에만 적용됩니다. 그러나 미시 대 거시 모델은 명백한 mesoscopic 모델링 접근 방식과 마찬가지로 정확하게 예측하는 데 크게 실패합니다. 이는 복잡한 동적 시스템의 일부 거시적 시스템 특성이 일관된 미시 대 거시 모델을 구축할 수 있는 능력이 부족하기 때문에 "강한 출현"에서 발생하는 현상(특성)의 예로 해석되어야 함을 시사합니다. 현상은 사전에 발생합니다. 이를 미시적 대 거시적 방식으로 예측할 수 없는 근본 원인은 일반적으로 "약한 출현"으로 분류되는 현상인 패턴 형성 과정으로 식별됩니다. 궁극적으로 이는 "약한" 출현과 "강한" 출현의 뚜렷한 범주를 구별하는 것이 원칙적으로 불가능할 수 있음을 시사합니다. 두 유형의 현상은 주로 시스템의 역학을 지배하는 동일한 피드백 루프의 일부일 수 있기 때문입니다.
1. 소개
창발적 특성을 나타내는 경향은 복잡한 시스템의 주요 특징입니다[ 1 ]. 출현은 생물학[ 2 ], 생태학[ 3 ], 신경학[ 4 ], 경제학[ 5 ], 사회 과학[ 6 , 7 ], 언어학[ 8 ] 및 철학[ 9 ]과 같은 다양한 과학 영역에서 연구되고 논의되어 왔습니다. ]. 이러한 영역에서 연구되는 모든 복잡한 시스템에서는 미시적 레이어에 있는 피드백 루프로 인해 거시적 시스템 레이어에서 창발 속성이 발생합니다. 예를 들어, 종종 미시적이고 국지적인 피드백 루프는 자기 조직화 프로세스를 유도하여 거시적 시스템 계층에 나타나는 패턴을 생성합니다.
복잡한 시스템에서 출현 현상의 존재와 타당성에 대한 중요한 논쟁이 있으며, 이는 출현의 두 가지 범주인 "약한 출현"과 "강한 출현"을 구별하는 제안으로 이어졌습니다[ 10 ] . 그러나 출현의 두 변종 사이의 이러한 구별은 논쟁을 해결하지 못했습니다. 한편으로는 이러한 구별 자체에 대한 의문이 제기되는 반면, 다른 한편으로는 단순히 '강력한 창발'이 존재하는지에 대한 논쟁이 지속되었다. 예를 들어, Mark Bedau는 "강력한 창발은 논리적으로 가능하지만 마술처럼 불편하다"고 말하고[ 10 ] Peter Corning은 "창출은 [...] 신비로운 개념도 아니고 환원주의 과학에 대한 위협도 아니다"라고 결론을 내립니다. [ 11 ] .
단순화를 위해 여기서는 "창발 현상", "약한 출현" 및 "강한 출현"이라는 용어가 현재 연구에서 사용되는 방법을 정의하기 위해 사용된 용어에 대해 간략하게 설명합니다.
1.1. 신흥 현상복잡한 시스템의 새로운 현상 특성은 종종 첫눈에 놀랍습니다. 이는 낮은 시스템 수준에서 작동하는 미세한 역학의 사소한 결과로 더 높은(거시) 시스템 수준에서 발생합니다. 사소하지 않은 점은 일반적으로 복잡한 시스템 내에서 특정 타이밍 계수(예: 인과 관계 효과의 지연)와 관련된 피드백 루프를 생성하는 비선형 구성 요소 상호 작용에서 발생합니다.
1.2. 약한 출현현상이나 시스템 특성은 처음에는 관찰자를 놀라게 할 수 있지만 나중에는 미시 대 거시 인과관계를 통해 쉽게 설명할 수 있습니다. 열심히 생각하거나 적절한 모델을 사용하면 그러한 현상을 먼저 관찰하지 않고도 예측할 수 있어야 합니다. 이는 기본적으로 시스템의 알려진 미시적 메커니즘을 기반으로 한 모델을 적용하여 거시적 수준의 이러한 현상을 예측할 수 있음을 의미합니다. 그러나 거시적 관찰로부터 매개변수화된 거시적 모델을 사용하여 이러한 현상을 예측하는 것은 창발적 현상을 "약하게 창발적"인 것으로 식별하는 데 충분하지 않습니다. 거시적 현상.
1.3. 강력한 출현이는 근본적인 미시적 메커니즘으로부터 일관된 모델(미시적 대 거시적 인과관계의 연쇄)에 의해 설명(사후) 및 예측(선험적)될 수 없는 창발적 현상 또는 시스템 특성입니다. 예를 들어 거시적 시스템 수준의 창발 현상이 미세한 구성 요소로 피드백되어 해당 동작을 변조하는 경우입니다. 이런 식으로 미시-거시-미시 인과관계의 폐쇄 루프가 발생합니다. 예를 들어, 미시적 메커니즘으로 쉽게 설명될 수 있는 강력한 미시 대 거시 효과가 있을 수 있으며, 전혀 긴급하더라도 약하게만 창발할 수 있습니다. 거시에서 미시로의 미묘한 피드백조차도 비선형 상호 작용 시스템에서와 같이 이러한 미시적 약한 창발 프로세스에 정확히 영향을 미칠 수 있습니다. 약한 피드백조차도 강력한 최종 효과를 가지며 예를 들어 위상 전환을 통해 시스템을 대체 상태로 유도할 수 있습니다. 따라서 이러한 피드백은 시스템의 신뢰할 수 있는 미시 대 거시 모델을 생성하는 능력을 손상시켜 이러한 무능력을 강한 출현의 특징으로 만들 수 있습니다.
처음에는 관찰된 현상이나 시스템 속성이 강력하게 출현한다고 주장하는 것이 예외적인 주장이라고 생각할 수도 있습니다. 따라서 그러한 주장은 예외적으로 강력한 증거에 의해 뒷받침되어야 한다고 추론할 수 있습니다. 그러나 이러한 첫 번째 직관과는 달리 정반대의 접근 방식이 필요한 것 같습니다. 여기에 제시된 연구는 실제로 창발적 특성을 해석하기 위한 약한 창발의 주장에 입증 책임이 있음을 입증하는 것을 목표로 합니다.
내 생각에, 증명되어야 할 정말로 예외적인 주장은 창발 현상을 약한 창발로 간주하는 것입니다. 이는 기본적으로 관찰된 창발 현상을 알려진 미시적 메커니즘으로부터 순전히 설명할 수 있다는 것을 의미하기 때문입니다 . 결과적으로 창발적 특성이 관찰되면 처음에는 이를 강한 창발로 간주한 다음 미시 대 거시 모델을 제시하여 이 가설을 반증하려고 노력해야 합니다. 이 미시 대 거시 모델은 현상을 설명하고 충분한 품질의 예측을 허용해야 합니다. 이 모델 구축 작업이 어려워질수록 관찰된 현상이 강한 출현의 예일 가능성이 더 커집니다. 실제 강한 출현의 경우 충분한 미시 대 거시 모델을 찾는 것이 불가능할 것입니다. 궁극적으로, 강한 창발을 해석하는 이러한 방식은 약하게 창발하는 현상이 강하게 창발하는 현상을 설명하는 구성요소가 될 수 있으며 그 반대의 경우도 마찬가지라는 것을 의미합니다.
복잡한 시스템이 순수한 미시적 모델로는 설명할 수 없는 창발적인 거시적 특징을 나타낸다는 사실은 Ising 모델[ 12 ]과 Turing 기계가 결합된 시스템의 결정 가능성 연구에서 Ising 모델 의 속성에 대해 입증되었습니다 [ 13 ].
여기에 제시된 연구는 Conway의 GoL(Game of Life) [ 14 ]과 같이 매우 간단한 메커니즘을 갖춘 복잡한 시스템에서 강력하게 창발되는 특성이 이미 관찰될 수 있음을 입증하는 것을 목표로 합니다. 이 게임은 발견된 지 수십 년이 지났지 만 다양한 커뮤니티 [ 15 ]. Marc Bedau의 독창적인 기사는 출현에 대한 GoL을 연구하고 약한 출현 유형의 현상인 이 시스템의 여러 특성을 설명합니다. 일반적으로 패턴 형성, 특히 다른 방식으로 작은 "펜토미노 구성"에서 시작하는 세포 집단의 성장 빈 세상 [ 10 ]. 이러한 현상과 시스템 특성은 모두 GoL의 간단한 미시적 규칙을 연구하고 모델링함으로써 쉽게 설명할 수 있습니다. 그러나 단순 GoL도 강력한 출현 사례인 현상을 생성합니까?
이 기사에서 조사된 가설은 언뜻 보기에 매우 사소해 보이는 특정 시스템 속성이 실제로는 가장 중요하지 않은 시스템 속성이자 강력한 출현의 예일 수 있다는 것입니다. 전 세계 인구 역학(시간에 따른 인구 밀도의 변화) ) 및 시스템이 수렴하는 장기 0이 아닌 인구 밀도(LTNPD)는 모두 GoL에서 관찰할 수 있습니다.
본 연구의 주요 가설은 순방향 시뮬레이션을 수행하여 쉽게 관찰하고 분석할 수 있는 시스템의 통계적 특성인 이러한 특성이 시스템을 시뮬레이션하지 않고 미시적 규칙을 분석하면 예측할 수 없다는 것입니다. 이러한 가설을 규명하기 위해 본 연구의 핵심 연구문제는 다음과 같다.(1)일반적으로 긴급하다고 간주되지 않는 GoL에 긴급한 거시적 특성이 있습니까?(2)"약한 출현"으로 이러한 시스템 특성을 설명하기 위해 미시에서 거시까지의 모델을 생각해 낼 수 있습니까?(삼)이러한 미시적 메커니즘을 통해 이러한 시스템 속성을 설명하는 중시적 모델을 고안할 수 있으며, 여전히 상향식 접근 방식을 따르면서 미시적 메커니즘에 의해 선험적으로만 정보를 얻을 수 있습니까?(4)이러한 현상은 거시적 사후 모델로 쉽게 예측할 수 있습니까?(5)이러한 속성과 모델링 접근 방식은 정확히 GoL은 아니지만 미시적 수준에서 유사하게 작동하는 다른 세포 자동 장치에 대해 어떻게 작동합니까?
2. 콘웨이의 인생 게임
다음에서는 본 연구에서 설명한 주장과 절차를 이해하는 데 필요한 측면을 설명하기 위해 GoL에 대해 매우 간략하게 설명합니다.
GoL은 너비가 X 이고 높이가 Y 인 유한한 격자형(격자) "세계"에서 작동합니다 . 여기에 제시된 연구에서 차원은 다음과 같습니다.세포. 모든 위치의 각 셀언제든지 단계는 다음 중 하나의 상태입니다.(사망) 또는 상태(살아 있는). 모든 시간 단계에서 셀은 표 1 에 설명된 규칙에 따라 상태를 업데이트합니다 . 이 업데이트는 동기식입니다. 따라서 모든 셀은 새로운 상태로 업데이트됩니다.이웃 셀의 상태와 이전 시간 단계의 자체 상태를 기반으로 합니다 . 이 업데이트를 위해 각 셀은 자체 상태와 무어 이웃 내 8개의 인접한 셀에 있는 "살아 있는" 셀의 수를 고려합니다[ 16 ]. 이 개별 "이웃 수"는 다음과 같이 표현됩니다.. 이웃 평가의 경우 가장자리 효과를 피하기 위해 세계가 토로이드(도넛 유형) 토폴로지로 래핑됩니다. 따라서 세계는 세포 수에 있어서 유한하지만 외부 가장자리는 없습니다. GoL의 정확한 업데이트 규칙은 표 1 에 나와 있습니다 . 기본적으로 다음을 제외한 모든 구성은 "죽은" 셀 상태를 생성합니다.(나)죽은 셀에 3개의 살아있는 이웃이 있으면 새로운 셀이 탄생합니다(표 1 의 녹색 프레임 ).(ii)세포는 2개 또는 3개의 살아있는 이웃 세포와 함께 살아 있습니다(표 1 의 파란색 프레임 ).
모든 세포가 상태를 성공적으로 업데이트한 후 각 시간 단계의 살아있는 세포 수는 다음과 같이 계산할 수 있습니다.전체 인구 중 살아있는 세포의 비율(인구 밀도)은 다음과 같이 계산할 수 있습니다..
그림 1 은 GoL 시뮬레이션 실행의 일반적인 예를 보여줍니다. 초기에 무작위로 분포된 살아있는 세포(이 경우 모든 세포의 20%)에서 패턴 형성 및 자기 조직화가 시작되어 여기에 표시된 2000 시간 단계의 런타임 이후 시스템의 모양을 형성했습니다. 인구밀도는 대략 인구밀도 수준으로 급격하게 감소했습니다. 이 기간의 4%와 "세계"는 다양한 구성의 살아있는 세포가 거주하는 여러 영역을 보여줍니다. 전체적인 풍경은 3가지 전형적인 지역 유형으로 특징지어질 수 있습니다. 일부 지역에는 살아있는 세포가 고갈되어 있고(빈 지역, A ) 일부 지역에는 고정된 패턴만 포함되어 있거나(블록, 벌집, 빵 등) 단순한 형태가 있습니다. 진동 패턴(예: 눈가리개)을 배치하여 인구 역학이 정지되었습니다("동결" 영역, B ). 동시에, 패턴 형성 프로세스가 집중적으로 작업하여 빠르게 변화하고 역동적인 패턴을 생성하는 일부 영역("생활" 영역, C )이 있습니다. 빈 영역( A )은 Wolfram 클래스 I에 해당하고, "동결" 영역은 Wolfram 클래스 II에 해당하며, "살아있는" 영역은 Stephen Wolfram이 지정한 명명법에 따라 Wolfram 클래스 IV에 가장 잘 해당 합니다 .
시간이 지남에 따라 이 세 가지 유형의 영역 사이의 크기 비율이 변경됩니다. 그들은 살아있는 세포의 무작위 시작 밀도에 따라 특정 인구 밀도로 수렴됩니다. 이는 관찰자에게 생물학적 밀도 의존적 인구 역학을 상기시키는 "수용 능력"에 의해 구동되는 과정을 암시합니다[ 18 ].
3. 생명 게임에서 나타나는 인구 밀도
GoL의 미세한 규칙 세트는 순전히 로컬 밀도 정보를 기반으로 합니다. 모든 단일 세포의 운명을 결정하는 것은 8개의 이웃 세포 집단 내 살아있는 세포의 일부일 뿐입니다. 이웃 내에서 이러한 살아있는 세포의 위치는 전혀 역할을 하지 않으며, 관찰된 패턴 형성이 이미 시스템의 흥미로운 특징이 되는 이유입니다. 미시적 규칙이 순전히 국소 밀도에 의존한다는 점을 감안할 때, 시간 경과에 따른 역학 및 잠재적 수렴점(평형, 고정점)과 관련하여 살아있는 세포의 전체 밀도는 이러한 규칙을 통해 쉽게 예측할 수 있어야 한다고 가정할 수 있습니다.
이러한 역학과 수렴 지점을 조사하기 위해 일련의 실험이 수행되었습니다. 이는 이 글의 후반부에서 강력한 출현의 후보로 제시된 거시적 특성이 실제로 GoL에 존재하는지 테스트하는 데 필요합니다.
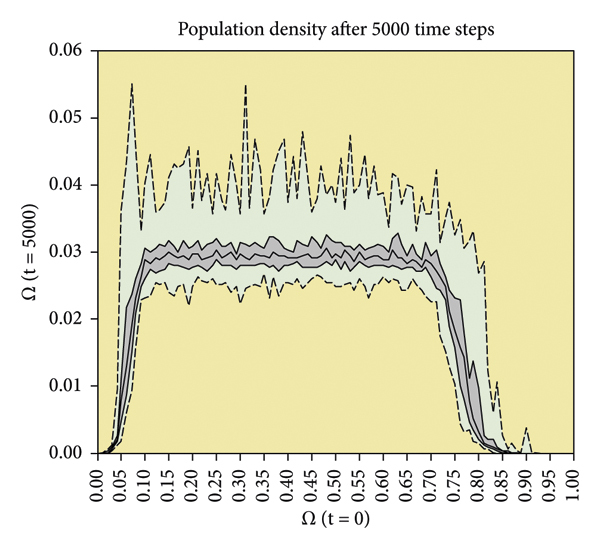
실험 1. 초기 밀도의 매개변수 스윕: GoL 시스템(크기 201 × 201)은 0%부터 다양한 밀도의 무작위 초기 모집단으로 초기화되었습니다., 100% 살아있는 세포로, 따라서, 1% 폭 단계씩 증가합니다. 각 설정은 살아있는 세포의 초기 밀도는 동일하지만 해당 세포의 무작위 분포는 다르게 30회 반복되었습니다. 따라서 실험 1 에서는 총 101개의 서로 다른 설정과 3030개의 시뮬레이션 실행이 수행되었습니다 . 각 시뮬레이션은 5000개의 시간 단계에 대해 실행되었습니다. 그 후, 생성된 살아있는 세포의 밀도를측정하여 LTNPD를 추정하였다. 그림 2 는 실험 1 에서 수행된 매개변수 스윕의 결과를 보여줍니다. 점선은 관찰된 결과의 최소값과 최대값을 나타내고, 회색 영역은 모든 결과의 50%를 포함하며, 굵은 검정색 선은 살아있는 세포의 특정 초기 밀도에 대한 중앙값 결과를 나타냅니다. 그림 2 는 시스템에 두 가지 중요한 위상 전환이 있음을 보여줍니다. 대략적으로 무작위로 분포된 살아있는 세포의 임계 밀도가 있습니다.
, 그 이하에서는 시스템이 완전히 멸종되는 경향이 있으므로. 밀도가 높을수록 덜 날카로운 상전이가 발생하여 최종 밀도가 대략적으로 감소하기 시작합니다. ~에이상, 위의 거의 모든 경우에 완전한 멸종을 보여줍니다.. 값 사이의그리고, 대다수의 실행에서 최종 밀도가 주변 값으로 수렴하도록 유도하는 시스템 체제가 작동하는 것 같습니다.. 모집단이 초기 밀도의 하한 임계 경계에 거의 정확히 수렴하는 것으로 보인다는 점은 주목할 만합니다. 흥미롭게도 GoL 시스템은 무작위 인구인 경우 지속 가능하지 않은 전 세계 인구 밀도로 스스로를 몰아갑니다. 이러한 결과는 일부 시작 조건에 대한 GoL [ 19 ] 의 시끄러운 비동기 업데이트 절차에 대한 연구에서 보고된 내용과 잘 일치합니다여기서는 LTNPD가 이러한 초기 조건에 어떻게 의존하는지에 대한 완전한 보기를 갖기 위해 가능한 초기 밀도의 전체 범위에 대해 더 미세한 단계로 매개변수 스윕을 수행했습니다. 이러한 관찰이 신흥 인구 역학에 하나 이상의 수렴 지점이 존재하기 때문이라는 것을 보여주기 위해 최종 인구 규모뿐만 아니라 인구의 역학을 연구하기 위한 두 번째 실험이 수행되었습니다.
실험 2. 여기서는 실험 1 에서 사용된 것과 동일한 GoL 시스템을 사용하여 4가지 다른 초기 조건을 테스트했습니다. 이러한 실행은 살아있는 세포의 무작위 초기 인구 밀도로 초기화되었습니다.. 다시, 각 설정은 동일한 초기 밀도로 30회 반복되었지만 살아있는 세포의 무작위 분포는 달랐습니다. 따라서 실험 2 에서는 총 120개의 실험이 시뮬레이션되었으며각 실험은 5000개의 시간 단계에 대해 수행되었습니다.
그림 3 은 실험 1 에서 보고 된이 아닌 최종 인구 밀도를 향한 인구 역학의 수렴이 분명히 있음을 보여줍니다.. 설정을 위해, 해당 실행에서 매우 다양한 결과가 달성되기 때문에 상황이 다른 것 같습니다. 그 결과 중 어느 것도 다른 초기 설정보다 인구 밀도가 더 높은 경향이 없습니다. 그러나 이렇게 낮은 초기 밀도로 인해 더 낮은 최종 인구 밀도도 가능한 것으로 보이며, 이는 이러한 낮은 밀도에 또 다른 수렴점(또는 그보다 더 많은 수렴점)이 존재할 수 있음을 나타냅니다. 그림 3
(a) 에 묘사된 개별 실행을 살펴보면 초기 정지 상태에 있는 실행(그림 3 의 직선 수평선)이 "동결"되고 빈 영역만 있는 구성에 도달했음을 알 수 있습니다. 이러한 실행은 여전히 매우 역동적인 실행(그림 3 의 흔들리는 선 )보다 낮은 LTNPD를 갖는 경향이 있으므로 여전히 "살아있는" 영역을 포함합니다.그리고, 동결 및 빈 실행보다 높은 것입니다. 그림 3 의 하위 그래프 오른쪽 열은 의최종 값 분포를 보여줍니다 . 이러한 분포는 표 2 에도 수치로 나와 있습니다. 두 실험에서 발견된 결과는 GoL 시스템이 장기적으로 인구가 수렴하는 0이 아닌 밀도 평형인 LTNPD에 적극적으로 접근한다는 것을 나타냅니다. 낮은 LTNPD에 접근하거나 심지어 시스템을 멸종으로 이끄는 극도로 낮거나 매우 높은 초기 인구 밀도를 제외하고 광범위한 무작위 초기 인구 밀도에 대해 동일한 LTNPD가 발견되었습니다. 질문은 다음과 같습니다. 모델이 이러한 일련의 행동을 질적으로 예측할 수 있습니까? 개체군 붕괴에 대해 관찰된 임계값과 0이 아닌 수렴점에 대해 관찰된 값을 그러한 현상을 단지 약하게 나타나는 것으로 분류하기 위해 순전히 알려진 미시적 규칙에 기초하여 정량적으로 해당 모델로 예측할 수 있습니까?
4. 거시적 모델
실험 2 에서 관찰된 역학의 거시적 모델을 구축하면 실험 1 의 결과도 예측할 수 있으며 기본적으로 간단한 작업입니다.
가장 쉬운 접근 방식은 실험 2의 관찰된 데이터를 사용하여 지수 붕괴 모델을 시뮬레이션 실행에 맞추는 것입니다.아마도 로그 모델을 사용하여 실행할 수도 있습니다.. 그러나 확실히 모든 초기 밀도에 대한 역학을 예측할 수 있는 단일 모델 접근 방식을 지원할 수 있는 함수가 있습니다 . 분명히, 관찰된 데이터에 일련의 매개변수를 적용하여 통계적 사후 모델을 매개변수화할 수 있으며, 이를 통해 초기 밀도에 대한 결과 밀도를 예측할 수 있습니다. 이러한 접근 방식은 거시적 데이터에만 적용되며 모델 구축 과정에서 어떠한 미시적 규칙도 고려하지 않습니다. 따라서 관찰된 현상과 관련하여 이 접근 방식은 GoL의 미시 대 거시 인과 관계에 대해 알려주지 않습니다.
시스템의 삶과 죽음의 과정을 닮은 또 다른 거시적 접근 방식은 알려진 생태학 문헌에서 유래한 거시적 모델을 사용하여 살아있는 세포의 집단 역학을 설명할 수 있습니다. 이러한 모델은 밀도 의존적 성장에 대한 고전적인 Verhulst 모델의 변형일 가능성이 높습니다[ 20 ].
방정식( 1 )에서 변수는 시간 단계에서의 살아있는 세포의 개체수이고 , 매개변수는 주어진 개체군의 성장률을 나타내며, 매개변수는 시스템의 주어진 수용 능력(예를 들어, 사용 가능한 공간에 의해 결정됨)을 나타냅니다. 단 두 개의 상수 매개변수. GoL은 개별 시간 단계에서 작동하는 자동 장치이므로 여기서는 개별 프로세스라는 표현을 의도적으로 선택했습니다. Verhulst 모델은 다음과 같은 불안정한 수렴점(평형, 고정점)을 갖는 것으로 알려져 있습니다.그리고 또 다른 안정적인 수렴 지점은 다음과 같습니다., , 및[ 21 , 22 ] 의 0보다 큰 모든 값에 대해 .
관찰된 결과를 자세히 살펴보면 최소 인구밀도가 있으며, 그 미만에서는 인구가 붕괴되거나 절대 멸종에 매우 가까워집니다. 이는 생물학자들에게 생물학적 집단의 유사한 역학을 설명하는 Allee 효과[ 23 ]를 상기시킬 수 있습니다. 예를 들어, 개체군 밀도가 낮아짐에 따라 동물이 짝짓기 파트너를 찾는 것이 더 어려워질 수 있습니다. 다른 예는 소규모 그룹(예: 포식자 탐지 및 회피)이나 다른 형태의 사회적 협력보다 대규모 그룹에서 사망 원인을 더 잘 피할 수 있다는 것입니다.
Allee 효과의 일반적인 모델은 다음과 같이 설명됩니다.
방정식 ( 2 )는 동일한 매개변수를 보유하고 특정 임계 인구 규모를 나타내는 추가 상수 매개변수를 제외하고 Verhulst 모델(방정식 ( 1 ))의 기본 개념을 따르며 , 그 이하에서는 성장률이 음수가 됩니다. Verhulst 모델의 Allee 효과 확장은 다음과 같은 안정된 수렴점(평형, 고정점)을 갖는 것으로 알려져 있습니다., 또 다른 안정적인 수렴 지점, 그리고 불안정한 평형점, , 및 의 0보다 큰 모든 값에 대해 .
이 모델은 GoL 시스템에서 낮은 초기 인구 밀도로 관찰된 위상 전이를 설명하지만 높은 초기 인구 밀도로 관찰된 위상 전이를 명시적으로 모델화하지는 않는다는 점은 주목할 만합니다. 그러나에서 거리가 증가함에 따라 증가합니다 . 따라서 시스템은 충분히 높은 매개변수 값을 사용하여 "언더슈트" 동작을 표시할 수 있는 것으로 알려져 있습니다 . 이는 이 거시적 모델에서도 매우 높은 인구가 시스템을 멸종점으로 몰아갈 수 있음을 의미합니다.
GoL이 현재 연구에서 관찰된 초점 특성에 관한 거시 대 거시 예측을 허용하는지 여부를 테스트하기 위해 GoL의 또 다른 시뮬레이션 실행 세트가 수행되었습니다. 각 설정은 30회 반복되었으며 시뮬레이션은 5% 폭 증분으로 0%에서 100%까지의 무작위 초기 인구 밀도 범위를 사용하여 5000개의 시간 단계에 대해 실행되었습니다. 그림 2 의 데이터세트는 역학 과정이 아닌 최종 모집단만 보고했고, 그림 3 의 데이터세트 에는 전체 역학이 포함되었지만 최대 20%의 초기 밀도에 대해서만 포함되었기 때문에 이러한 추가 시뮬레이션 실행이 필요했습니다. 이러한 매개변수 스윕의 결과는 그림 4 (a)의 하위 그림에 표시됩니다. 이는 그림 2 와 3 에 표시된 데이터와 잘 일치하므로 추가 확인이 가능합니다.
그림 4 의 맨 위 하위 그래프는 시스템의 매우 구체적인 초기 동작을 표시하는 10개의 첫 번째 시간 단계를 보여줍니다. 그렇지 않으면 데이터의 수평 확장으로 인해 표시되지 않습니다. 가운데 행의 하위 그래프는 전체 런타임 동안의 인구 밀도 역학을 보여주고, 아래쪽 행의 하위 그래프는 초기 인구 밀도와 최종 인구 밀도를 보여줍니다. 여기의 매개변수 스윕은 그림 2 에 표시된 것보다 훨씬 더 거칠기 때문에 위상 전환이 거기만큼 정확하게 캡처되지는 않습니다. 그러나 거시적 모델을 이러한 데이터에 쉽게 적용할 수 있는 경우 이 데이터는 테스트에 충분합니다.
그림 4 (b) 의 하위 그래프는 모델 피팅 절차에서 찾은 최상의 매개변수 설정을 사용한 모델의 해당 예측을 보여줍니다. 이 피팅의 경우 운반 능력은 다음과 같이 설정되었습니다.201 × 201 세포의 격자 크기에 있는 살아있는 세포는 그림 2 와 3 에서 관찰된 LTNPD와 매우 유사한 값입니다 . 더 낮은 밀도 임계값에서의 인구 붕괴가 LTNPD 바로 아래의 인구 밀도에서 관찰됨에 따라 Allee 효과 임계값의 값은 다음과 같이 설정되었습니다.살아있는 세포. 이러한 고정 매개변수 값을 사용하면 유일한 자유 매개변수 값은 R 이며, 이는 모든 초기 밀도와 전체 시간에 걸쳐 시뮬레이션 데이터와 모델 예측 간의 제곱 차이를 최소화하는 방식으로 체계적으로 변경되었습니다. 에 대한 적절한 값이 다음에서 발견되었습니다., 이 값과 마찬가지로 거시적 모델은 모든 초점 거시적 시스템 속성을 예측할 수 있습니다. 이는 매우 높은 밀도와 매우 낮은 밀도에서 인구 붕괴를 모두 포착하고 주요 인구 역학을 포착하며 GoL의 관찰된 LTNPD에 가까운 값으로의 수렴을 포착합니다. 이러한 예측의 품질은 왼쪽 열의 하위 그래프와 오른쪽 열의 하위 그래프를 비교하여 그림 4 에서 확인할 수 있습니다
Allee 효과 확장(식 2 )을 사용하여 일반 바닐라 버전의 Verhulst 모델을 GoL에서 관찰된 인구 데이터에 맞추는 것은 쉬웠지만 , 이는 이 특정 규칙 세트가 이러한 현상을 생성하는 이유를 알려주지 않습니다. 이 기사에서 연구된 초점 속성의 출현(유형)과 관련하여 이 모델 피팅은 거시적 시스템 계층만 작동하기 때문에 그 자체로는 도움이 되지 않습니다. 모델은 거시적 사고로 구성되었으며, 거시적으로 도출된 사후 데이터에만 적합되었습니다. 그러나 시스템의 창발적 특성을 실제로 이해하기 위해 이러한 모델링 접근 방식 은 사후에 맞추는 대신 미시적 규칙 세트에서 , 및 선험적으로 직접적으로 매개 변수 값 을 도출할 수 있는 경우에만 도움이 될 것입니다. 관찰된 거시적 데이터로부터.
5. 현미경 모델
다음에서는 이러한 거시적 모델 매개변수( , , ) 가 시스템의 시뮬레이션 없이 알려진 규칙 세트로부터 선험적 프로세스에서 직접 파생될 수 있는지 확인하기 위해 미시적 모델을 개발하고 분석합니다. 분명히 Verhulst 모델과 Allee 효과에 대한 확장이 수렴하는 것으로 알려진 매개변수 값은 GoL 시스템 시뮬레이션에서 관찰되는 LTNPD와 일치해야 합니다. 거시적으로 쉽게 관찰되는 매개변수의 값을 미시적 대 거시적 인과관계를 확립하기 위해 미시적 규칙에서도 예측할 수 있습니까? 이를 위해 특정 규칙에서 나타나고 이러한 규칙에서 직접 선험적으로 예측할 수 있는 시스템의 피드백에 초점을 맞춘 접근 방식이 선택됩니다.
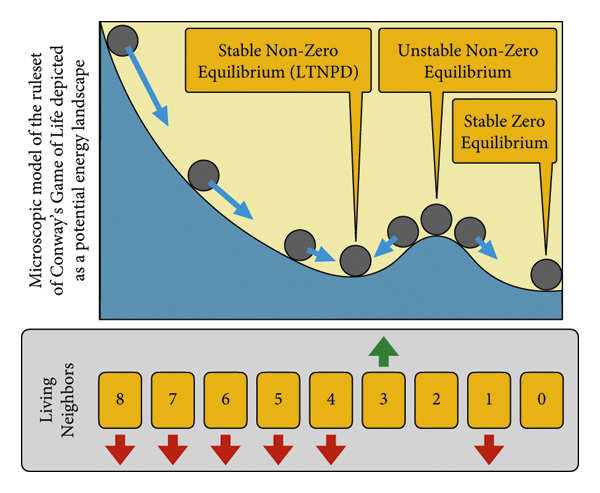
그림 5는 이러한 미세한 접근 방식의 간단한 그래픽 표현을 보여줍니다. 여기서 화살표는 무어 근처에 있는 살아있는 세포의 로컬 밀도를 기반으로 하는 세포의 개별 업데이트를 기반으로 인구가 어느 방향으로 발전하는 경향이 있는지 보여줍니다. 이는 개별 세포 행동이 전체 살아있는 세포 밀도의 변화로 이어지지 않는 세 가지 뚜렷한 사례를 나타냅니다.(1)평균적으로 4~8개의 살아있는 이웃이 있는 세포는 우선적으로 죽습니다. 따라서 인구 밀도는 결과적으로 감소하는 반면 (평균) 살아있는 세포 3개 크기의 살아있는 이웃 크기는 새로운 살아있는 세포의 탄생으로 이어질 수 있습니다. 이는 인구밀도를 높이는 데 기여할 것입니다. 이는 셀이 (평균적으로) 3~4개의 이웃을 갖는 조건에서 평형 밀도가 있음을 나타냅니다. 이는 8개의 이웃 그리드 셀 집단에서 평균 3.5개의 살아있는 세포의 안정적인(규제된) LTNPD를 암시하며, 이는 그리드 셀당 3.5/8 = 0.4375개의 살아있는 세포 밀도에서 LTNPD가 예상되어야 함을 나타냅니다. 시스템은 43.75%의 안정적인 평형 인구 밀도를 나타냅니다.(2)평균적으로 2개의 살아있는 이웃이 있는 세포는 시스템의 그리드 셀당 2/8 = 0.25개의 살아있는 세포로 이웃당 2개의 살아있는 세포에서 평형을 구성해야 하며, 미세한 역학에 존재하는 이 밀도에 대한 명확한 규제는 없습니다. 이는 불안정한 평형 인구 밀도가 25%임을 나타냅니다.(삼)평균적으로 2개 미만의 살아있는 이웃이 있는 세포는 우선적으로 죽습니다. 따라서 인구 밀도는 0으로 감소합니다. 이는 안정적인 평형 인구 밀도가 0%임을 나타냅니다.
미시적 규칙에 대한 이러한 해석은 GoL 시스템의 C 운반 능력이 대략적으로 가정되어야 함을 보여줍니다. 43.75%인 반면, 실제로 시뮬레이션 실험에서는 약 2.9%로 관찰되었습니다(그림 2 및 3 ). 분명히 미시 대 거시 예측은 한 자릿수 이상 실패합니다.
또한 거시적 모델의 임계값 매개변수와 관련하여 미시적 모델이 제시하는 값이 크게 잘못될 수 있습니다. 개체군이 멸종되는 불안정한 티핑 포인트는 그리드 셀당 2/8 = 0.25개의 살아있는 세포 근처에 있는 것으로 제안됩니다. 따라서 밀도는 25%인 반면, 그림 2 에서는 밀도가 3% 정도인 것으로 나타났습니다.
그 외에도 또 다른 거시적 측면은 질적으로도 공제되지 않습니다. 높은 초기 밀도에서의 두 번째 상 전이는 실험 1 에서 관찰됩니다 (그림 2 ). 미시적 모델은 초기 인구 밀도가 70%인 인구(세포당 평균 5.6명의 살아있는 이웃)가 장기적으로 "정상" 인구 밀도 수준에서 번성하는 반면, 75% 밀도의 초기 인구(평균)에 대한 유용한 정보를 제공하지 않습니다. 세포당 6개의 살아있는 이웃)은 이미 심각한 어려움을 겪고 있으며 밀도가 80%(세포당 6.4개의 살아있는 이웃)를 가진 개체는 이미 멸종 위기에 처해 있습니다.
6. Mesoscopic 모델
미시적 모델이 인구 역학을 10배 이상 정확하게 예측할 수 없는 이유는 미시적 규칙이 패턴 형성으로 이어져 인구를 서로 다른 Wolfram 범주의 영역으로 구조화한다는 사실에서 비롯됩니다(그림 1 ) . 이러한 개별 영역 유형은 서로 다른 밀도 특성을 가지며 밀도가 추가 밀도 개발에 영향을 미친다는 것을 그림 2 에서 확인했습니다 .
분명한 선택은 역학을 지배하는 피드백을 묘사함으로써 이러한 면적 역학을 포착하는 메조스코픽 모델을 추구하는 것입니다. 여기서도 이 접근법은 이 모델이 미시적 시스템 규칙 세트에서 선험적인 방식으로 미시적 프로세스에 의해서만 구성되고 매개변수화될 수 있는 경우에만 도움이 됩니다.
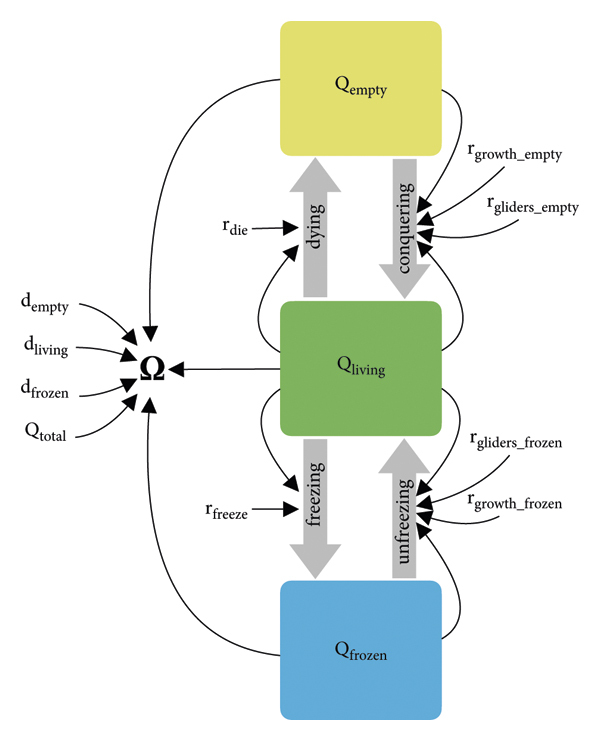
이러한 mesoscopic 모델에 대한 간단한 접근 방식은 GoL의 세계를 표시된 세 가지 영역 유형에 따라 내부에서 발생하는 주요 역학(비어 있음, 얼어붙음, 살아 있음)을 특징으로 하는 철저한 사분면 세트로 세분화하는 것입니다. 그림 1 에서 . Mesoscopic 모델은 한 유형에서 다른 유형으로의 사분면 전환을 설명할 수 있습니다. 예를 들어, 시스템 동역학 모델 구축 접근법[ 24 ]에 따르면, 그림과 같이 저량 및 흐름 모델링 접근법[ 25 ]의 개념과 함께 상미분 또는 차이 방정식(ODE 또는 OΔE) 시스템을 구현할 수 있습니다. 6 .
그림 6 의 색상 상자는 해당 모델의 주요 시스템 변수, 즉 특정 상태의 사분면 수량을 나타냅니다. 회색 두꺼운 화살표는 한 상태에서 다른 상태로의 사분면 전환을 나타냅니다. 검은색 가는 화살표는 시스템 구성요소의 인과적 종속성을 나타냅니다. 상자가 없는 텍스트 요소는 모든 상수 매개변수와 유일한 기타 시스템 변수를 나타냅니다 . 이 초점 거시적 변수는 이들 3개 사분면 모집단의 비율, 이들 사분면이 나타내는 인구 밀도( , , ) 및 사분면 의 절대 수를 기반으로 예측할 수 있습니다. 네 가지 고유한 흐름은 한 유형에서 다른 유형으로의 사분면 전환을 설명하여 시스템의 질량 보존을 보장합니다. 이러한 흐름은 다음과 같이 모델링됩니다. (나)"살아있는" 사분면의 일부는 두 계수 와 에 의해 설정된 비율로 얼거나 비워질 수 있습니다 . 이 프로세스는 그림 6 에 왼쪽 두 흐름을 가리키는 두 개의 얇은 검은색 화살표로 표시되어 있으므로 기존의 동결 및 빈 사분면 모집단과 독립적입니다 . 이러한 흐름은 및 의 영향을 받지만 및 의 영향을 받지 않습니다 .(ii)"동결된" 사분면 중 일부는 다시 살아날 수 있습니다(동결 해제). 이는 "살아있는" 사분면에서 발생하는 활동으로 인해 발생할 수 있습니다. 이러한 상호의존성은 대량행동법 용어로 가장 잘 표현됩니다., 두 계수의 합을 곱합니다. 계수는살아있는 세포 집단이 사분면 경계를 넘어 증가하고 인접한 사분면에서 "살아있는" 과정을 다시 시작하는 속도를 나타냅니다. 또 다른 계수는"살아있는" 사분면이 "동결된" 사분면에 들어가 그곳에서 "살아있는" 과정을 다시 트리거하는 글라이더 또는 기타 움직이는 구조물을 생성하는 속도를 나타냅니다.(iii)유사하게 빈 사분면의 일부는 두 가지 유사한 과정을 통해 생명으로 다시 정착될 수 있습니다. 즉, 성장을 통해 인접한 "살아 있는" 사분면에 의해 정복되거나( ) 잠재적으로 먼 "살아 있는" 사분면에서 유래하는 두 개의 글라이더에 의해 부트스트랩 됩니다 ( ). 두 프로세스 모두 집단 소송법 용어로 가장 잘 모델링됩니다.왜냐하면 "살아있는" 사분면과 상호작용하는 빈 사분면이 모두 필요하기 때문입니다.
이 모델, 특히 생명체가 거주하는 패치(사분면)가 무인도를 "정복"하는 방법을 설명하기 위한 대량 행동법 접근 방식의 사용은 생물학적 정착 및 확산 과정을 예측하는 데 사용되는 고전적인 Levins 모델을 밀접하게 따르고 있습니다[ 26 ] .
살아 있는 패치와 죽은 패치만 고려한 Levins 모델과 달리, 여기서 Mesoscopic GoL 모델은 "동결" 서식지 상태도 고려하여 확장됩니다. 그러나 기본 모델링 구조와 개념은 기존의 "살아있는" 사분면과의 상호작용을 통해서만 살아날 수 있기 때문에 "살아있는" 사분면 모두에 대해 유사합니다. 결과적으로 모델은 네 가지 다른 평형을 갖게 됩니다. 세 가지 불안정한 평형은 다음과 같습니다., ~에, 그리고 또한. 0이 아닌 유량 계수를 사용하면 사분면 모집단에서도 안정적인 평형이 유지됩니다..
메소스코픽 모델은 미시적 모델보다 더 복잡하지만 두 단계 전이를 완전히 예측하는 데 실패합니다. 이 메소스코픽 모델 구조는 Allee 효과 유형 동작이나 고밀도에서의 모집단 붕괴를 예측할 수 없기 때문입니다. 이를 구현하려면 모델을 추가 용어로 확장해야 하며, 이전에 이미 설명한 것처럼 미시적 규칙에서 올바르게 도출할 수 없는 매개변수 및 를 다시 전달 해야 합니다 .
이 mesoscopic 모델에는 숫자 값이 필요한 10개의 매개변수가 있습니다. 즉, 저량 및 흐름 모델의 4개 흐름에 대해 위에서 언급한 6개의 계수( 그림 6 의 6개의 " r " 매개변수 ), 사분면이 유형을 지정하는 3개의 인구 밀도( , , ) 표시되며, 사분면의 총 개수가 표시됩니다 .
미시 대 거시 모델로 유용하려면 모든 매개변수 값이 미시적 메커니즘에서 결정되어야 합니다. 의 사소한 결정 외에도 미시적 사고에서는 두 개의 밀도 매개변수( 및 ) 만 파생될 수 있습니다 . 의 값은 0.0이어야 하고 0.4375 정도여야 합니다. 이 밀도는 게임이 진행되는 영역에 대해 이미 미시적 모델에서 공제되었기 때문입니다. 생명은 매우 역동적인 방식으로 자신의 상태를 적극적으로 처리하고 있습니다. 나머지 밀도 추정량 과 6개 공정 계수 모두 미시적으로 알려진 추론에서 공제하는 것이 불가능해 보입니다. 이러한 영역에서 관찰된 밀도(그림 1 )는 "동결" 영역이 가질 수 있는 소위 "최대 밀도 정물"(MDSL)보다 훨씬 낮으며, 이는 57.1%로 확인됩니다[ 27 ] . 이는 그림 5 에 묘사된 현미경 모델에 의해 (평균적으로) 8개의 이웃 세포 중 2개가 "살아 있는" 불안정한 평형으로 제안된 25%보다 낮습니다 . 따라서 GoL 시뮬레이션이 진행되는 동안 "동결" 영역이 갑자기 수렴되는 관찰 밀도에 대한 유용한 예측을 제안하는 미세한 규칙 세트 해석에서 비롯된 지식이 없습니다.
미시적 규칙에서 흐름 계수를 도출하는 것이 다음으로 해결되지 않은 문제입니다. 글라이더 생산 속도, 글라이더 간 충돌 속도, 글라이더 대 동결 구조물 충돌 속도를 도출할 방법도 없습니다. 또한 필요에 따라 미시적 규칙으로부터 직접 동결, 성장 및 사망 비율을 도출할 수도 없습니다.
상향식 모델 구축 작업은 점점 더 토끼굴로 내려가는 것처럼 느껴집니다. 그림 5 에 묘사된 순수 현미경 모델의 경우처럼 한 가지 문제 대신, 이제 그림 6 에 묘사된 모델에서 해결해야 할 7가지 별도의 문제가 있습니다 . 필요한 각 매개변수 값을 미시적으로 도출하려면 특정 하위 모델이 필요합니다. 이러한 7개의 하위 모델에는 더 많은 하위 모델 등을 구축해야 할 가능성이 높습니다. 이는 GoL의 인구 역학 및 LTNPD를 예측할 수 있는 일관된 마이크로-메소-매크로 모델을 만드는 것이 원칙적으로 불가능하다는 지표일 수 있습니다. 이는 이러한 새로운 현상이 강력한 출현에서 비롯된다는 것을 의미합니다.
이러한 문제가 있는 매개변수화 외에도 mesoscopic 모델에서 발생하는 다른 문제가 있습니다. 모델 구축에 적용되는 개념은 미시적 지식에서 비롯된 것이 아닙니다. 예를 들어, “동결된” 지역이 다시 살아나기 위해서는 “살아있는” 지역과의 상호작용이 필요하다는 사실은 단순한 미시적 규칙을 연구하는 것만으로는 선험적으로 도출될 수 없습니다. 시스템의 시뮬레이션 실행을 연구하여 얻은 지식입니다. 따라서 이 모델 구축에는 선험적 지식이 아닌 사후 지식이 이미 통합되어 있습니다.
7. 다른 변형 연구
이 섹션에서는 대체 설정을 고려하고 앞서 언급한 결과가 초기 조건의 특정 아티팩트인지 특정 규칙 세트인지에 대해 질문합니다. 지금까지 GoL은 여기에 제시된 연구에서 살아있는 세포의 무작위 분포 분포를 사용하여 항상 연구되었습니다. "R-펜토미노" 구성[ 28 ]이라는 간단한 구조는 비어 있는 세계에서 단 5개의 인접한 살아있는 세포로 시작하여 인상적인 성장을 보이는 것으로 알려져 있습니다 . 이를 통해 GoL이 초기 인구 밀도와 관련하여 매우 낮은 시작점에서도 관찰된 LTNPD에 접근하는지 테스트할 수 있습니다.
또한 GoL의 규칙 세트와 매우 밀접하게 관련된 다른 셀룰러 오토마타가 마이크로-매크로 모델을 사용하여 LTNPD를 직접 정확하게 예측하는 데 유사한 실패를 보이는지 여부를 다음에서 조사합니다.
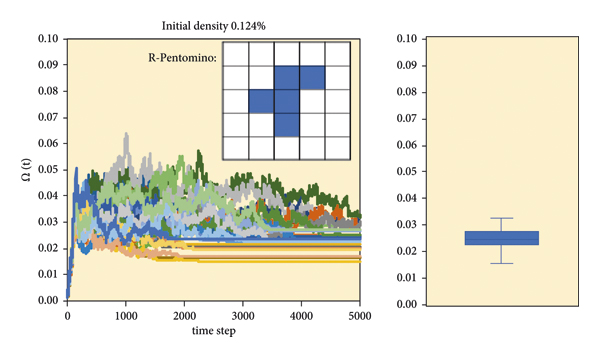
7.1. 드물게 분산된 R-Pentomino 모집단에서 시작된 역학 연구본 분석에서는 이전 실험과 동일한 설정을 사용하였다. 유일한 차이점은 이번에는 10개의 R-펜토미노 구성이 처음에 그리드의 임의 위치에 배치되었고 다른 모든 셀은 "죽은" 상태로 설정되었다는 것입니다. 이는 초기 밀도에 해당합니다.(0.124% 밀도). 그림 7 은 R-pentomino 구성의 한 인스턴스, 30회 시뮬레이션 실행의 모집단 역학 및 접근된 LTNPD의 최종 분포를 보여줍니다. 이 낮은 초기 시작점에서도 이전 실험에서 얻은 결과와 매우 유사한 인구 밀도에 적극적으로 접근한다는 것을 분명히 볼 수 있습니다. 시스템이 수렴하는 관측된 중앙 밀도는 다음과 같은 것으로 나타났습니다.관찰된 IQR은 0.004였습니다. 이전 실험과 마찬가지로, 결국 "살아있는" 영역이 여전히 있는 실행은 이미 "동결된" 빈 영역으로 완전히 구성된 실행보다 더 큰 최종 인구를 달성했습니다. 이는 여기서 수행된 관찰이 무작위 초기 분포의 인공물이 아니라는 것을 나타냅니다. 그러나 밀도 의존적 성장 역학은 "실행 가능한" 방식(예: 소수의 R-펜토미노 사용)으로 구성되는 경우 매우 낮은 시작 모집단에도 적용됩니다.
7.2. 밀접하게 관련된 셀룰러 오토마타 연구GoL의 LTNPD가 출현 유형과 관련하여 얼마나 "특별한"지 조사하기 위해 약간 조정된 규칙 세트를 사용하여 여러 세포 자동 장치를 테스트했습니다. 이러한 실험의 주요 연구 질문은 다음과 같습니다. 이러한 세포 자동자가 수렴하는 LTNPD에 관한 미시 대 거시 모델 예측도 실패합니까?
7.2.1. 변종 A: 더 많은 이웃과의 번식이 세포 자동 장치의 규칙은 GoL에서 물려받은 세 명의 살아있는 이웃과 함께 탄생하는 것 외에도 네 명의 살아있는 이웃이 있는 죽은 세포가 살아난다는 점에서 GoL과 다릅니다. 표 3 은 단색 프레임으로 새로운 규칙을 나타내고, GoL에서 상속된 규칙은 점선 프레임으로 표시됩니다.
그림 8 은 이 세포 자동 장치가 완전히 "동결된" 미로 같은 패턴으로 수렴되는 것을 보여줍니다. GOL에 대한 그림 5 에 표시된 것과 유사한 이 규칙 세트의 미세한 모델은 4~5개의 살아있는 이웃 사이의 LTNPD를 예측하며 다음 값을 가리킵니다.. 이는 대략 인구 밀도로의 수렴을 제안합니다. 56%. 이 세포 자동 장치에 대한 5000단계 긴 시뮬레이션을 30회 반복한 결과 LTNPD의 중앙값은또는 대략. 51%로 순수 현미경 모델로 예측한 값에 매우 가깝습니다.
7.2.2. 변형 B: 더 적은 수의 생존 이웃으로 번식하고 더 좁은 범위에서 생존이 세포 자동 장치의 규칙은 GoL의 경우처럼 두 개의 살아있는 이웃이 있는 죽은 세포가 세 개의 살아있는 이웃이 있는 죽은 세포가 아닌 살아난다는 점에서 GoL과 다릅니다. 또한, 3개의 살아있는 이웃이 있는 세포는 죽게 되지만, 그러한 세포는 GoL에서 살아남게 됩니다. 표 4 는 단색 프레임으로 새로운 규칙을 나타내고, GoL에서 상속된 생존 규칙은 점선 프레임으로 표시됩니다.
그림 9 는 이 세포 자동 장치가 때때로 살아있는 세포의 단기적인 집합과 함께 매우 역동적인 눈보라와 같은 패턴으로 수렴한다는 것을 보여줍니다. GOL에 대한 그림 5 에 표시된 것과 유사한 현미경 모델은 2개와 3개의 살아있는 이웃 세포 사이의 LTNPD를 예측하며 다음 값을 가리킵니다.. 이는 대략 인구 밀도로의 수렴을 제안합니다. 31%. 이 세포 자동 장치에 대한 5000단계 긴 시뮬레이션을 30회 반복한 결과 LTNPD의 중앙값은또는 대략의 밀도. 27%로 이는 다시 순수 현미경 모델로 예측한 값에 매우 가깝습니다.
7.2.3. 변종 C: 더 많은 이웃과 더 넓은 생존 범위를 통한 번식이 세포 자동 장치의 규칙은 GoL의 경우처럼 4개의 살아있는 이웃이 있는 죽은 세포가 살아 있고 3개의 살아있는 이웃이 있는 죽은 세포가 살아난다는 점에서 GoL과 다릅니다. 1~4개의 살아있는 이웃이 있는 살아있는 세포는 살아남는 반면, GoL에서는 2~3개의 살아있는 이웃이 있는 세포만 살아남습니다. 표 5 는 단색 프레임으로 새로운 규칙을 나타내고, GoL에서 상속된 생존 규칙은 점선 프레임으로 표시됩니다.
그림 10 은 이 세포 자동 장치가 흥미로운 행동을 보인다는 것을 보여줍니다. 처음에는 매우 역동적이지만 영역은 수평 또는 수직 줄무늬 패턴으로 "동결"되고 그 사이에 수지상 같은 빈 패턴이 형성되어 가장자리를 따라 높은 활동을 보여줍니다. 천천히, 빈 수지상 영역을 희생시키면서 동결된 영역이 커집니다. 결국 이들 수지상 부위의 추억의 흔적은 결국 텅 빈 섬으로 남게 되고, 결국에는 얼어붙고 텅 빈 부위만 남는다. GOL에 대한 그림 5 에 표시된 것과 유사한 미세한 모델은 4~5개의 살아있는 이웃 세포 사이의 LTNPD를 예측하며 다음 값을 가리킵니다.. 이는 대략 인구 밀도로의 수렴을 제안합니다. 56%. 이 세포 자동 장치에 대한 5000단계 긴 시뮬레이션을 30회 반복한 결과 LTNPD의 중앙값은또는 대략. 48%로 이는 다시 순수 미시적 모델로 예측한 값에 다소 가깝습니다.
다른 두 가지 변형과 비교하여 변형 C 로 얻은 결과에서 이 자동 장치는 최종 구성에 대해 더 흥미롭고 더 복잡한 과도 현상을 나타냅니다. 따라서 모든 변형 중에서 미시적 예측에서 가장 큰 편차를 보여준다는 사실은 흥미로운 오토마타가 일반적으로 마이크로 대 매크로 예측에서 더 높은 오류를 표시하여 이 오류를 잠재적인 흥미를 나타내는 신호로 바꿀 수 있다는 잠재적인 경향을 암시합니다. (강하게) 출현.
8. 논의 및 결론
Conway의 Game of Life는 첫 출판 이후 50년 동안 엄청난 과학적 관심을 불러일으켰습니다. 예를 들어 Andrew Adamatzky가 편집한 GoL 40주년 기념 책은 GoL과 그 주변에서 수행되는 매우 풍부하고 다양한 연구를 보여줍니다. [ 15 ]: 예를 들어 연구는 고전적인 GoL 자체 에 대해 수행됩니다. , GoL이 잘못된 비동기 업데이트 체제를 어느 정도까지 견딜 수 있는지 연구함으로써 [ 19 ]. 또한 대체 변형도 종종 생성되고 연구됩니다. 이러한 GoL 변종에는 대체 규칙 세트가 있거나[ 29 ] 연속 상태로 작동[ 30 ]하여 문헌에 보고된 많은 사례 중 몇 가지만 언급합니다. 최근 인상적인 "레니아(Lenia)" 시스템은 연속 공간을 이동하는 글라이더와 유사한 개체인 "오븀(Orbium)" 생물이 GoL의 규칙에서 미시적으로 파생될 수 있음을 보여주었습니다. [ 31 ] 레니아를 고급 연속 공간으로 전환 합니다 . GoL의 우주 변형. 가장 두드러지게, GoL은 그 자체로 튜링 완전하고 GoL 내부에 범용 튜링 기계를 구축하는 등 예외적인 구조를 구축할 수 있는 것으로 밝혀졌습니다[ 32 ] . 한편, GoL과 동등한 3D를 찾는 것은 지속적인 과제입니다[ 33 , 34 ].
Mark Bedau의 연구는 약한 출현과 강한 출현의 구별을 제시했으며, GoL의 패턴 형성 과정과 펜토미노 성장만을 특징으로 합니다. 이는 (올바르게) 이러한 프로세스를 약한 출현 유형으로 식별합니다 [ 10 ]. 이 프리젠테이션과 그 주장은 독자에게 GoL에 강한 출현 현상이 없다는 인상을 주게 됩니다. 비록 이것이 명시적으로 언급되지는 않았지만 일반적으로 강한 출현은 의심됩니다.
이러한 인상과는 대조적으로, 여기에 제시된 연구는 GoL의 여러 속성이 실제로 강력한 출현을 위한 좋은 후보임을 보여줍니다. 즉, 무작위 모집단이 붕괴되는 두 가지 임계값, GoL에서 "동결" 영역이 발전하는 밀도, 그리고 가장 눈에 띄는 것은 지구 시스템이 대부분의 시작 상태에서 수렴하는 0이 아닌 장기 인구 밀도입니다.
그것들을 강한 창발의 사례로 제안하는 이유는 다음과 같습니다: 간단하고 순전히 선험적으로 정보를 얻은 미시적 모델도 아니었고, 단순하고 순전히 선험적으로 정보를 얻은 중시적 모델도 어떤 식으로든 유용한 힌트를 전달할 수 있는 것으로 밝혀졌습니다. 이러한 신흥 시스템 속성의 수치 값. 이와 대조적으로 생태학적 모델링 문헌에는 잘 알려져 있고 적합한 거시 대 거시 모델이 존재합니다. 이 거시적 인구 모델의 매우 기본적인 일반 바닐라 변형조차도 그림 2 , 3 및 7 에 표시된 데이터에 설명된 대로 GoL의 조사된 모든 거시적 동작을 이미 매우 잘 포착할 수 있다는 것이 입증되었습니다 . 여기서 중요한 점은 다음과 같습니다. 이는 거시적으로 도출된 데이터를 기반으로 사후 방식으로 쉽게 수행할 수 있지만, 직접적인 미시 대 거시 인과관계를 통해 지식을 수집하는 것은 여기서도 충분히 작동하지 않습니다. 알려진 미시적 규칙은 거시적 모델에 적합한 매개변수 값에 대해 사전에 알릴 수 없습니다. 그리고 사후 모델 피팅 후 거시적 모델을 잘 예측할 수 있는 값은 미시적 모델 분석에서 제시하는 값이 아닙니다. 따라서 다양한 모델 구축 시도 전반에 걸쳐 여기에 보고된 이러한 모든 관찰의 결과로, 미시 대 거시 모델 구축에서 관찰된 어려움 또는 심지어 무능력은 이러한 조사가 모델의 글로벌 시스템 속성을 조사했다는 지표일 수 있다고 제안됩니다. GoL은 실제로 강력한 출현 유형입니다.
이러한 관찰을 반영하여 여기에 제시된 연구는 제안을 전개하지만 물론 GoL 시스템의 이러한 거시적 특성이 강력한 출현 유형일 수 있다는 확실한 증거를 제공하지는 않습니다. 이 제안은 충분한 예측 품질을 갖춘 직접적인 미시 대 거시 모델을 찾을 수 없다는 점뿐만 아니라 적절한 메조스코픽 모델을 검색할 때 "토끼 구멍 아래로 내려가는" 유형의 개발에 의해 뒷받침됩니다. . 일반적으로 미지수(필요한 매개변수)의 수는 모델 구축이 하향식 방식으로 거시에서 미시로 깊어질수록 증가하고, 거시적 모델이 미시적 모델보다 더 추상적이기 때문에 상향식 모델 구축에서는 감소합니다. 놀랍게도 GoL의 모델 구축에서는 이와 반대되는 경향이 발견된다. 미시적 모델에 필요한 모든 매개변수는 규칙 세트에서 쉽게 파생될 수 있었고 결과 예측만 틀렸지만 중시적 모델은 결정적으로 필요한 7개의 시스템 매개변수에 대한 매개변수화에 이미 실패했습니다. 이러한 계수를 매개변수화하려면 더욱 구체적인 하위 모델이 필요하며, 결과적으로 더 많은 매개변수화 문제가 발생합니다.
논의된 시스템 속성이 실제로 강력하게 창발적인 경우 이는 기본적으로 강력한 창발의 범주에 때때로 호출되는 "마법"이나 "형이상학"이 필요하지 않음을 의미합니다. 대조적으로, 이는 GoL과 같은 결정론적 시스템에서도 복잡한 인과 중심 시스템에서 나타날 수 있습니다.
전체 거시적 상태를 순전히 국소적인 미시적 동역학으로 환원할 수 없는 것은 마이크로-거시-미시 피드백으로 인해 발생할 수 있습니다. 예를 들어, 국부 밀도는 알려진 미시적 규칙(그림 5 )에 따라 결정되며 국부 밀도는 "비어 있음", "동결" 또는 "살아 있음"으로 특징지어지는 국부적 영역의 행동 상태에 영향을 미칩니다. 그러나 미세한 역학은 그러한 지역 유형에서 상당히 다른 입력 패턴을 발견합니다. 따라서 기능적 출력으로 다양한 후속 역학을 생성합니다. 이는 결국 더 높은 시스템 계층에서 발견되는 역학(예: 성장, 부패 및 해당 지역 영역의 상호 작용 속도)에 영향을 미치고 궁극적으로 특정 종류의 더 큰 영역(사분면)의 비율을 결정합니다. 이러한 사분면 유형의 공간 분포.
이러한 mesoscopic 상호 작용은 그림 6 에 설명된 것처럼 고유한 상위 수준 메커니즘을 발전시킬 수 있으며 , 이는 그림 2 및 3 에 표시된 것처럼 궁극적으로 거시적 동작을 생성할 수 있습니다 .
예를 들어 사분면이 해당 유형을 변경함으로써 더 높은 수준의 구성 요소가 동적으로 변경됨에 따라 이는 해당 로컬 미세 메커니즘이 작동하는 입력 구성으로 다시 피드백됩니다. 미세한 규칙은 로컬 밀도에 대해 작동하고 다양한 유형의 사분면이 다른 수준으로 수렴됩니다. 밀도의. 따라서 시스템 내에는 분명히 마이크로-메조-마이크로 피드백이 있으며, 이는 궁극적으로 거시적 시스템 수준에도 반영됩니다. 이러한 메조스코픽 모델 중 여러 개가 서로 내부에 중첩될 수 있고 모두 크기가 증가하는 사분면을 나타낼 수 있기 때문입니다. 따라서 시스템은 무한한 그리드 크기에 대해 잠재적으로 무한한 수의 메조스코픽 시스템 레이어를 갖는 마이크로-메소 - 매크로-메소 - 마이크로 피드백 시스템으로 볼 수 있습니다.
GoL 시스템의 유한한 격자 크기를 사용하더라도 그림 6 에 묘사된 메조스코픽 모델은 더 큰 사분면 내부에 포함된 더 작은 사분면의 중첩 모델을 통해 재귀적으로 구현될 수도 있습니다. 이러한 방식으로 시스템의 여러 Mesoscopic 레이어를 수학적으로 표현할 수 있습니다. 그러나 다중 메조스코픽 레이어의 이러한 접근 방식은 매우 다른 이유로 인해 맨 아래, 로컬 미시 레이어까지 완전히 내려갈 수도 없고, 맨 위의 전체 거시 레이어까지 완전히 올라갈 수도 없습니다.
시스템 레이어의 맨 아래에서 그림 6 에 묘사된 스톡 및 흐름 모델은 규칙 세트를 통합하기 위해 이 시스템 레이어를 설명하기 위해 그림 5 에 묘사된 미세한 모델이 필요하기 때문에 3×3 셀의 사분면에 의미 있는 방식으로 적용할 수 없습니다. GoL을 전체 모델로 통합하고 이렇게 작은 사분면 크기로 인해 "동결된" 사분면과 "살아있는" 사분면 사이에 필요한 차별을 허용하지 않을 가능성이 높습니다. 이러한 모델링 접근 방식은 미시적 수준으로 완전히 내려가기 전에 이미 중단될 가능성이 높습니다. 예를 들어 4 × 4 또는 5 × 5 그리드 셀의 사분면 크기는 사분면 유형을 결정하기에는 너무 작습니다.
시스템 레이어의 맨 위에 있는 그림 6 에 표시된 스톡 및 흐름 모델은 사분면 크기가 너무 커지자마자 중단됩니다. 예를 들어, 최상위 거시적 수준에서 이러한 스톡 및 흐름 모델은 시간이 지남에 따라 유형이 변경되는 단일 사분면만 처리합니다. 이러한 구성에서 흐름은 값만 가질 수 있으므로 매우 특별하고 극단적인 방식으로 작동합니다 . 따라서 4개의 흐름 중 하나만 가질 수 있고 3개의 저류 중 하나만 각 시간 단계에서 값을 보유할 수 있습니다 . 이진수 값만 허용하는 모델에서는 mesoscopic 모델의 핵심 개념이 깨질 것입니다. 예를 들어 두 흐름 모델링의 대량 행동 법칙은 깨질 것입니다. 왜냐하면 단 하나의 주식만이 0이 아닌 값을 가지기 때문입니다. 따라서 관련된 모든 흐름은 항상 0으로 유지되고 모든 시스템 역학은 0에서 정지됩니다., 최신. 여기서도 이러한 모델링 접근 방식은 최상위 거시적 레이어로 올라가기 전에 이미 중단됩니다. 전체 그리드 공간을 나타내는 전체 시스템 사분면을 나타내는 몇 개의 사분면만으로는 이미 의미 있는 방식으로 작동하지 않습니다.
일반적으로 마이크로-거시-마이크로 피드백 루프는 상향 및 하향 인과관계를 부과하며 강력한 출현을 나타내는 지표로 해석될 수 있습니다. 피드백 루프는 루프의 구성 요소로 패턴 형성 과정(약하게 나타나는 현상)을 가지고 있습니다. 이는 그러한 구별이 전혀 유용한지 의문을 제기합니다. 전체 피드백 루프에 대한 약하게 창발적인 구성 요소의 기여가 다양할 수 있다는 점을 고려하면 강한 창발 루프 내부의 약한 창발의 가중치는 가변적입니다. 이는 이것이 이분법이 아님을 시사합니다. 그것은 오히려 출현의 강도가 떨어질 수 있는 스펙트럼이 될 것이며, 잠재적으로 미시 대 거시 예측이 실패하는 오류의 크기와 상관관계가 있을 것입니다.
이러한 마이크로-거시-마이크로 루프는 연구된 셀룰러 오토마타의 변종에도 존재합니다. 예를 들어, 변종 A 와 C 는 매우 명확한 패턴 형성 과정을 보여 주며 일시적인 경우 GoL과 같이 세 가지 유형의 영역이 모두 나타납니다. 또한 GoL과 유사하게 이러한 변종은 결국 얼어붙고 빈 영역만 있는 상태가 됩니다. 이러한 모든 미시적 및 거시적 유사성에도 불구하고 그들의 미시적 대 거시적 예측은 시뮬레이션 실행의 측정된 거시적 결과에 매우 잘 들어맞습니다. 이는 GoL이 전체 규모에서 실패하는 것과는 매우 대조적입니다. 이는 GoL의 규칙 어딘가에 아직 밝혀지지 않은 숨겨진 게임 체인저가 있음을 나타냅니다. 매우 초기의 "동결" 변종 A 와 C 나 항상 매우 역동적인("살아 있는") 변종 B 모두 간단하고 신뢰할 수 있는 미시 대 거시 예측을 제공하는 데 문제가 없습니다. 신뢰할 수 있는 마이크로 대 매크로 예측조차 방해하는 GoL 규칙 세트는 무엇입니까? 변형 규칙이 GoL 규칙의 약간의 변형에 불과하다는 점을 감안할 때 이는 시스템의 주요 속성인 마이크로 대 매크로 예측 가능성에 있어 매우 흥미로운 차이입니다.
이 기사의 주요 주장을 그래픽으로 요약한 것이 그림 11 에 나와 있습니다 . 이는 여러 모델 구축 변형이 GoL(또는 강력한 출현을 보여줄 수 있는 다른 시스템)의 특정 시스템 계층을 고려하는 방법을 보여 주며, 현재 연구에서 논의된 접근 방식을 그래픽으로 나타냅니다. GoL의 경우 예시 시스템으로서 거시적 모델은 미시적 규칙에서 직접적으로 성공적으로 매개변수화될 수 없으며 직접적인 미시 대 거시 예측도 성공적으로 이루어질 수 없습니다. 또한 특별히 맞춤화된 (하위) 모델을 사용하여 미시적 시스템 층과 거시적 시스템 층 사이의 중시적 시스템 층을 덮는 것은 매개변수 공간의 폭발로 인해 그리고 이러한 (하위) 모델 사이의 시스템 경계에 오류가 축적되어 실패할 가능성이 높습니다. 더 나쁜 것은 모든 모델이 자체 레이어별 모델 매개변수를 예측하기 위해 다른 모델을 필요로 하기 때문에 모델 구축의 무한 루프에 빠질 가능성이 있다는 것입니다.
궁극적으로 이러한 모든 고려 사항은 마이크로 대 매크로 예측이 불가능한 근본 원인이 마이크로-거시-마이크로 피드백의 존재 자체가 아니라 오히려 약하게 창발되는 기능(패턴 형성)이 구동한다는 사실임을 시사합니다. Mesoscopic 시스템 계층에서 발생하는 프로세스로 인해 신뢰할 수 있는 모델을 만들 수 없는 방식으로 이러한 마이크로-거시-마이크로 피드백 시스템이 발생합니다. 이는 정확히 이 모델 구축 불가능성이 강력한 출현을 식별하는 데 적합한 구별 기능이 될 것임을 시사합니다.
강력한 출현을 위한 유망한 후보로 밝혀진 GoL의 시스템 특성이 (단지) 약하게 출현하는 패턴 형성만큼 훌륭하지 않다는 것은 놀라운 일입니다. 즉, 가장 흥미로운 시스템 속성은 여기에서 눈에 잘 띄지 않게 숨겨져 있으며 간과되어 결과적으로 과거에도 대규모로 과소 연구되었습니다. 이는 패턴 형성 과정과 그에 따른 후속 결과가 인상적이어서 연구를 더 쉽게 그리고 더 많이 유치할 수 있기 때문일 것입니다.
예를 들어, GoL이 인공 지능(AI) 및 기계 학습(ML) 연구의 분투하는 영역에 어떻게 영감을 주었는지 살펴보면 비슷한 그림이 발견됩니다. 거시적으로 파생된 데이터(예: 형성될 알려진 패턴)를 기반으로 하는 훈련 실행에서 미시적인 규칙을 학습할 수 있는 AI를 개발하기 위한 많은 노력이 있다는 것은 놀랍습니다[35 ] . 그에 비해 훨씬 더 어려운 문제를 다른 방법으로 해결하려는 문헌은 아직 없는 것 같습니다. 이는 AI가 시간이 지남에 따라 시스템을 반복적으로 시뮬레이션하지 않고 순수하게 미세한 입력(규칙 세트)으로부터 셀룰러 오토마타의 예측하기 어려운 거시적 결과를 예측하도록 하는 것입니다. 그런 다음 훈련된 모델은 GoL과 여기에 제시된 변형에 대해 신뢰할 수 있는 미시적 거시적 예측을 할 수 있어야 합니다. 이러한 예측이 모든 규칙 세트에 걸쳐 충분히 다양한 시작 조건에 대해 유지된다면 실제로 이 AI는 예측 문제를 해결하고 잠재적으로 강력한 출현이 가능한 시스템 속성을 단지 약한 출현의 경우로 식별했을 것입니다.
이러한 AI 기반 마이크로-매크로 모델 구축 방법은 자동화된 출현 감지기 및 분류기 역할을 하는 데도 유용할 것입니다. 첫째, 복잡한 동적 시스템의 시뮬레이션은 패턴 인식 AI로 분석할 수 있습니다. 패턴 형성 과정을 감지하면 이 시스템은 긴급 속성을 표시하는 것으로 표시될 수 있습니다. 그런 다음 AI를 구축하는 모델은 변경된 규칙 세트의 올바른 예측과 함께 규칙 세트에서 바로 시뮬레이션 없이 이 시스템의 거시적 동작을 올바르게 예측하는 예측 모델을 학습하려고 시도할 수 있습니다. 이 AI가 모든 시스템에 대해 올바른 예측을 학습하면 이 시스템은 약한 창발 속성만 나타내도록 분류될 수 있습니다. 그러나 AI의 미시 대 거시 모델 학습이 초점 시스템에서는 실패하고 다른 변형에서는 잘 작동하는 경우 이 시스템은 강력한 출현을 위한 매우 유망한 후보로 자동으로 표시될 수 있습니다. 유사하게, 이러한 기술을 사용하면 단일 특정 초점 시스템에 집중하고 다양한 거시적 시스템 속성을 자동으로 탐색하고 출현 유형에 따라 분류할 수 있습니다.
흥미로운 신흥 속성을 자동으로 찾기 위한 이러한 계산 AI 알고리즘의 필요성은 미세한 시스템 매개 변수를 통한 대규모 매개 변수 스윕 또는 많은 양의 인스턴스에서 미세한 매개 변수를 변경하는 진화 계산 알고리즘에 유용할 것입니다. 첫 번째 사례의 예는 복잡한(GoL과 유사한) 원시 입자 시스템을 사용하여 수행된 대규모 매개변수 스윕입니다[ 36 ]. 두 번째 경우의 예는 "군집 화학"이라는 복잡한 시스템을 사용하여 수행된 진화적 접근 방식입니다. 흥미롭고 새로운 복잡한 시스템을 찾기 위한 "개방형" 진화 접근 방식을 고려할 때 흥미로운 시스템 동작의 자동 감지도 매우 편리할 것입니다 [ 37 ].
GoL과 같은 시뮬레이션 시나리오 대신 물리적으로 구현된 시스템을 살펴보면 여기에 제안된 기준을 사용하여 경험적 관찰과 비교하여 미시 대 거시 예측을 확인함으로써 시스템이 하드 출현의 특징을 보이는지 여부를 알 수 있습니다. 예를 들어, 물리화학적 상호작용은 지구 환경 요인(예: 온도)과 미시적 변수(예: 배열의 원자 사이의 거리 또는 기타 패턴)에 따라 달라지는 거시적 수준 특성(예: 분해 지점)과 관련된 상 전이를 나타낼 수 있습니다. 미세한 국지적 상호작용 메커니즘을 지배하는 인과적 결과. 이러한 상전이가 마이크로 대 매크로 모델을 통해 정성적으로 또는 정량적으로 정확하게 시뮬레이션될 수 있다면 이는 원자 수준에서 규칙적인 패턴 형성 및 재구성이 발생하더라도 어려운 출현이 발생하지 않을 가능성이 높다는 지표로 볼 수 있습니다. 마이크로와 매크로 사이의 성공적인 상향식 연결의 예는 예를 들어 분자 역학 및 재료 상호 작용에 대한 화학 연구에서 찾을 수 있습니다 [ 38 , 39 ].
출현과 현상을 미시 대 거시 모델로의 환원 가능성에 관한 질문은 모든 복잡한 적응 시스템에서 발생합니다 [ 40 ]. 따라서 그들은 우주, 일반적인 생명 현상, 인간 두뇌, 그리고 상호 작용하는 사람들 사이에서 나타나는 사회와 문화적 특성을 연구하는 가장 흥미로운 과학의 최전선에서 제기되는 연구 질문과 연결됩니다. GoL은 복잡한 동적 시스템의 매우 단순한 장난감 모델일 뿐이지만, 깨지기 어려운 속성을 연구하면 복잡한 시스템에서 발생하는 현상을 해결해야 하는 다른 모든 영역에서 상당한 진전을 이루는 데 도움이 될 수 있습니다.
가장 이해하기 어려운 속성이 전혀 눈에 띄지 않고 오랫동안 눈에 잘 띄지 않는 것처럼 보이는 반면, 약한 형태의 창발은 눈에 띄게 두드러지며 훨씬 더 많은 연구를 끌어들이는 사실이 나를 궁금하게 만듭니다. GoL뿐만 아니라 다른 복잡한 적응 시스템에도 아직 감지되지 않은 그러한 속성의 사례가 얼마나 많이 있습니까?
데이터 가용성
이 연구를 뒷받침하는 데 사용된 데이터는 합당한 요청이 있을 경우 해당 작성자로부터 ZIP 파일로 묶인 CSV 또는 Excel 파일로 제공됩니다.
이해 상충
저자는 이해상충이 없음을 선언합니다.
감사의 말
이 작업은 그라츠 대학의 Field of Excellence COLIBRI(기초 연구 및 혁신의 복잡성)의 지원을 받았습니다.
참고자료
-
G. Andrighetto, M. Campenni, F. Cecconi 및 R. Conte, 규범 출현의 복잡한 루프: 상호 작용 에이전트 및 사회 현상을 시뮬레이션하는 시뮬레이션 모델 , Springer, Tokyo, pp. 19–35, 2010.
-
M. Gardener, "수학 게임: John Conway의 새로운 솔리테어 게임 "life"의 환상적인 조합," Scientific American , vol. 223, 아니. 4, pp. 120–123, 1970.
보기: Google 학술 검색 -
A. Adamatzky, Ed., Game of Life Cellular Automata , Springer, London, vol. 2010년 1월 1일
-
S. Wolfram, 새로운 종류의 과학 , Wolfram media, Champaign, IL, USA, vol. 5, p. 2002년 130호.
-
N. Fatès, 인생은 비동기성에 저항하는가? Game of Life Cellular Automata , Springer, London, pp. 257–274, 2010.
-
PF Verhulst, “Recherches mathématiques sur la loi d'accroissement de la 인구,” Journal des Économistes , vol. 12, 페이지. 276, 1845.
보기: Google 학술 검색 -
I. Karsai, T. Schmickl 및 G. Kampis, 생태 및 사회 시스템의 탄력성과 안정성 , Springer, Berlin, 2020.
-
A. Ford 및 FA Ford, 환경 모델링: 환경 시스템의 시스템 역학 모델 소개 , Island press, 워싱턴 DC, 미국, 1999년.
-
G. Chu, KE Petrie 및 N. Yorke-Smith, 최대 밀도 정물을 해결하기 위한 제약 프로그래밍 Game of Life Cellular Automata , Springer, London, pp. 167–175, 2010.
-
D. Eppstein, 실물과 같은 세포 오토마타의 성장과 붕괴 Game of Life Cellular Automata , Springer, London, pp. 71-97, 2010.
-
F. Peper, S. Adachi, J. Lee, 생명 게임의 변형 Game of Life Cellular Automata , Springer, London, pp. 235–255, 2010.
-
BWC Chan, Lenia 및 확장된 우주 인공 생명 회의 논문집 , MIT Press, 미국 케임브리지, pp. 221–229, 2020.
-
P. Rendell, "Conway의 생명 게임에 사용되는 보편적인 Turing 기계", 2011년 고성능 컴퓨팅 및 시뮬레이션에 관한 국제 회의 간행물 , pp. 764-772, IEEE, 이스탄불, 터키, 2011년 7월.
보기: Google 학술 검색 -
C. Bays, "3차원 생명 게임의 많은 새로운 규칙 발견에 관한 메모", Complex Systems , vol. 16, 아니. 4, p. 381, 2006.
보기: Google 학술 검색 -
JM Springer 및 GT Kenyon, "신경망이 인생의 게임을 배우는 것은 어렵습니다.", 2021 신경망 국제 합동 컨퍼런스(IJCNN) 회보 , 1–8페이지, IEEE, 중국 선전, 2021년 7월.
보기: Google 학술 검색 -
H. Sayama, 군집 화학 II의 개방형 진화 추구: 자동화된 개체 수확을 통한 장기 역학 분석 인공 생명 회의 논문집 , MIT Press, 미국 케임브리지, pp. 59–66, 2018.
-
M. Gell-Mann, 복합 적응 시스템 , Routledge, 영국, 영국, pp. 11–24, 2018.
저작권
'생명공학' 카테고리의 다른 글
| 만성질 환자의 영양 관리 (2) | 2023.11.20 |
|---|---|
| 심근 변형에 따른 심장아밀로이드증의 구별 (1) | 2023.10.28 |
| 의생명과학 대학원 (1) | 2023.09.22 |
| 존스홉킨스대학교 - 화학 및 분자 생물학, 박사 (0) | 2023.08.30 |
| Ixodes scapularis (0) | 2023.08.12 |